(b) Find out the current through the cell and voltage across it from the given circuit diagram.

Subject:
Physics
Author:
babykins
Created:
1 year ago

Answers 2

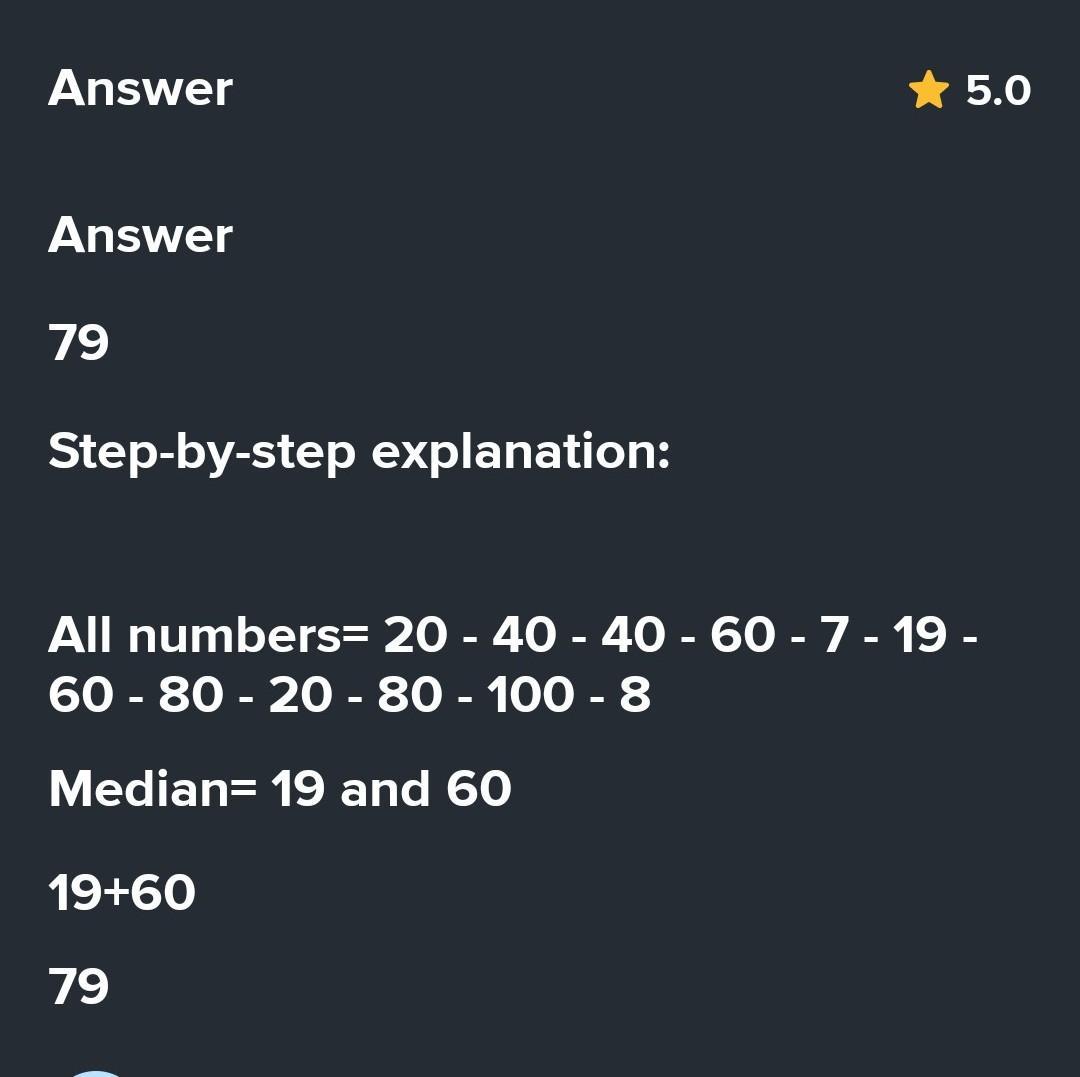
Answer:

answer will be 60 Amphere for sire

Author:

keltonhk4t
Rate an answer:
0

Answer:

The current through the cell and voltage across it is 4 A and 2 volts respectively.

Explanation:

The current and voltage across the cell will be calculated through the ohms law. Which is given as,

[tex]V=IR[/tex] (1)

Where,

V=potential difference

I=current through the circuit

R=resistance of the circuit

From the question we have,

R₁=3Ω

R₂=2Ω

R₃=10Ω

R₄=10Ω

The internal resistance of the cell(r)=0.5

The potential difference of the circuit(V)=12volt

The resistors R₁ and R₂ are connected in series. So, their net resistance will be,

[tex]R_s=R_1+R_2[/tex]

[tex]R_s=2+3=5\Omega[/tex] (2)

Now the resistors R₃, R₄ and [tex]R_s[/tex] are connected in parallel. So,

[tex]\frac{1}{R_p}=\frac{1}{R_3} +\frac{1}{R_4} +\frac{1}{R_s}[/tex] (3)

By substituting all the required values in equation (3) we get;

[tex]\frac{1}{R_p}=\frac{1}{10} +\frac{1}{10} +\frac{1}{5}[/tex]

[tex]\frac{1}{R_p}=\frac{1+1+2}{10}[/tex]

[tex]R_p=\frac{10}{4}[/tex]

[tex]R_p=2.5\Omega[/tex] (3)

The net resistance of the circuit is,

[tex]R=R_p+r[/tex] (4)

By substituting the values in equation (4) we get;

[tex]R=2.5+0.5[/tex]

[tex]R=3\Omega[/tex] (5)

By using equation (1) the current through the cell is calculated as,

[tex]12=I\times 3[/tex]

[tex]I=\frac{12}{3}[/tex]

[tex]I=4A[/tex] (6)

The voltage across the cell(e) will also be calculated using equation (1) which is given as,

[tex]e=I\times r[/tex] (7)

By placing the values in equation (7) we get;

[tex]e=4\times 0.5[/tex]

[tex]e=2Volt[/tex]

Hence, the current through the cell and voltage across it is 4 A and 2 volt respectively.

#SPJ3

Author:

brown sugar3zj7
Rate an answer:
9

(b) Find out the current through the cell and voltage across it from the given circuit diagram.

Answers 2

If you know the answer add it here!

Can't find the answer?

Other Physics Questions

(b) Find out the current through the cell and voltage across it from the given circuit diagram. ​

Answers 2

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

Other Physics Questions

(b) Find out the current through the cell and voltage across it from the given circuit diagram.