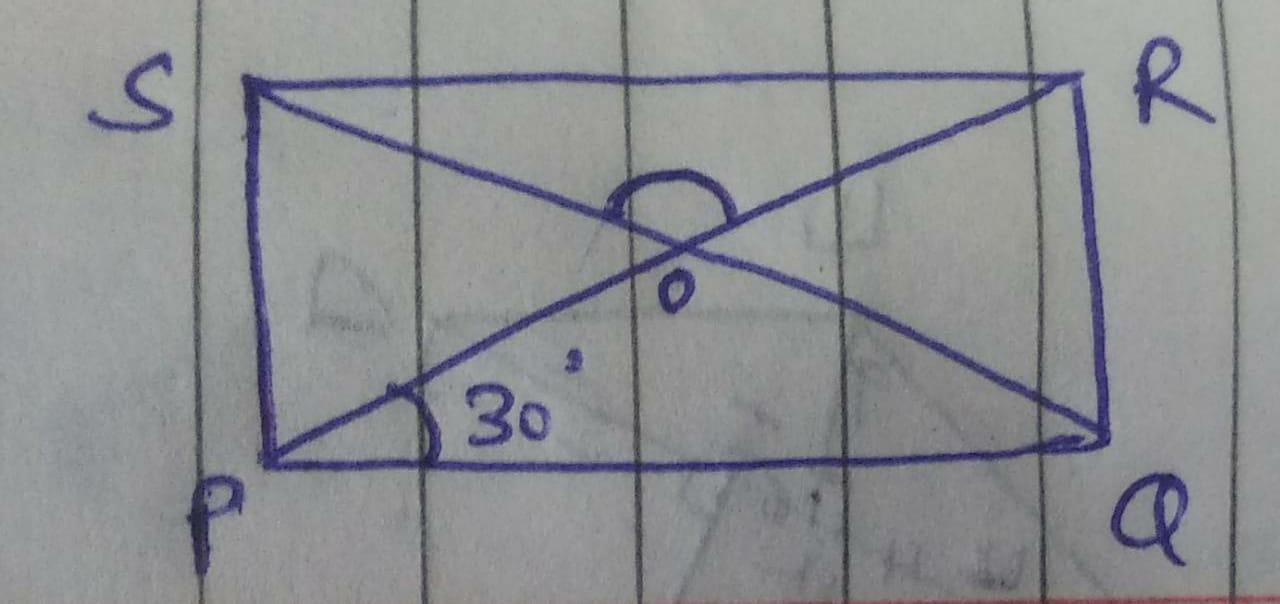
in this que hunterman please mark me as brainliest ans say me thankyou and vote me as 5.0what is electricity
-
Subject:
World Languages -
Author:
miguel -
Created:
1 year ago
Answers 1
Answer:
electricity is the flow of electrical power or charge .
Explanation:
Pranjal pls mark me a brainliest
Hope it helps u

-
Author:
desiraecooley
-
Rate an answer:
18
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years