The maximum height reached by a projectile is equal to half of the range of projectile. If the initial velocity of projection was 20 m/s, then what was maximum height reached? (g = 10 m/S2)​

• We know a relation

• R tanθ = 4 H

Given: R = 2H ; u = 20m/s

• That implies, H/R = tanθ/4

⇒ H/2H = tanθ/4

• 1/2 = tanθ /4

We'll get tanθ= 2

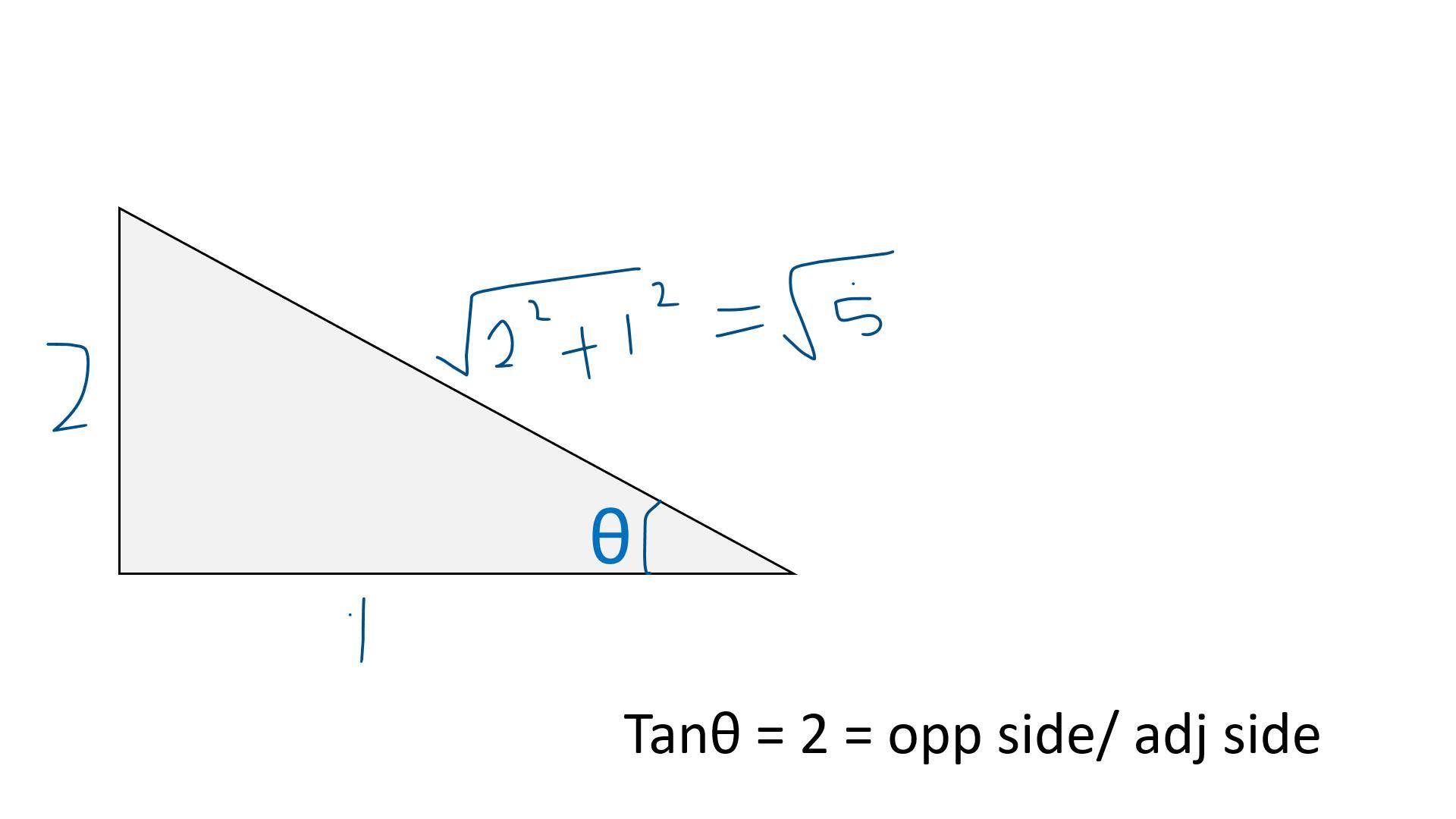
Now we'll draw a triangle to calculate all trignometric frnctions easily

You can see the triangle in the Attachment.

From the triangle sinθ = [tex]\frac{2}{\sqrt[]{5} }[/tex] ; cosθ = [tex]\frac{1}{\sqrt[]{5} }[/tex]

H = [tex]\frac{u^2sin^2theta}{2g}[/tex]

H = [tex]\frac{400 * (\frac{2}{\sqrt{5} })^2 }{20} = \frac{4}{5} *20 = 16m[/tex]

⇒Anagh :}

Given:

Initial velocity [tex]=20m/s[/tex]

Acceleration due to gravity [tex]=10m/s^{2}[/tex]

To find:

Maximum height reached by the projectile.

Solution:

Step 1

For a projectile released from a point with some initial velocity as [tex]u[/tex] and the angle made by the projectile with the horizontal,

The height reached by the projectile [tex]H=\frac{u^{2} .sin^{2}\alpha }{2g}[/tex]  

The range of the projectile is [tex]R=\frac{u^{2}.sin 2\alpha }{g}[/tex]  

Step 2

Now,

According to the question,

The height reached by the projectile is equal to half the range of the projectile. Hence, we get

[tex]\frac{u^{2} .sin^{2}\alpha }{2g}=\frac{1}{2}\frac{u^{2}.sin 2\alpha }{g}[/tex]

[tex]sin^{2} \alpha =sin2\alpha[/tex]

[tex]sin^{2} \alpha =2.sin\alpha .cos\alpha[/tex]

[tex]sin\alpha =2.cos\alpha[/tex]

[tex]tan\alpha =2[/tex]

We know,

[tex]sec^{2} \alpha =1+tan^{2} \alpha[/tex]

[tex]sec^{2} \alpha =5[/tex]

Hence,

[tex]cos^{2} \alpha =\frac{1}{5}[/tex]

We know,

[tex]sin^{2} \alpha =1-cos^{2} \alpha[/tex]

[tex]sin^{2} \alpha =\frac{4}{5}[/tex]

Step 3

Now,

We have, [tex]u=20m/s[/tex]   [tex];[/tex] [tex]sin^{2} \alpha =\frac{4}{5}[/tex]    [tex];[/tex] [tex]g=10m/s^{2}[/tex]

We get, the height reached by the projectile as

[tex]H=\frac{u^{2} .sin^{2}\alpha }{2g}[/tex]

[tex]H=\frac{(20)^{2}(\frac{4}{5} ) }{2(10)}[/tex]

[tex]H=16m[/tex]

Final answer:

Hence, the maximum height reached by the projectile is 16 meter.