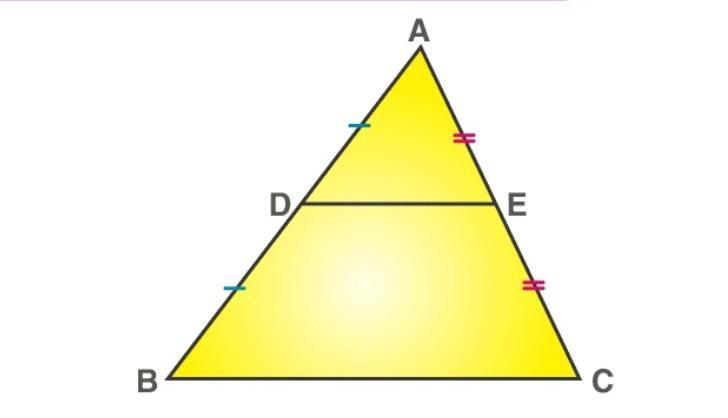
The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.
Consider the triangle ABC, as shown in the above figure,
Let E and D be the midpoints of the sides AC and AB. Then the line DE is said to be parallel to the side BC, whereas the side DE is half of the side BC; i.e.
DE = (1/2 * BC).
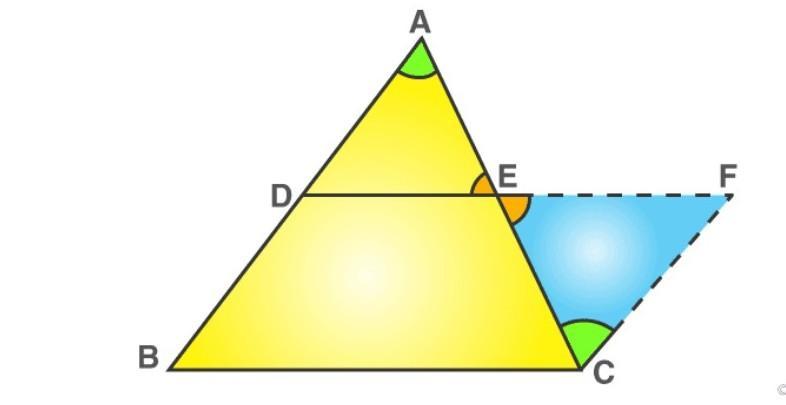
Construction- Extend the line segment DE and produce it to F such that, EF = DE.
In triangle ADE and CFE,
EC = AE —– (given)
∠CEF = ∠AED (vertically opposite angles)
∠DAE = ∠ECF (alternate angles)
By ASA congruence criterion,
△ CFE ≅ △ ADE
Therefore,
∠CFE = ∠ADE {by c.p.c.t.}
∠FCE= ∠DAE {by c.p.c.t.}
and CF = AD {by c.p.c.t.}
∠CFE and ∠ADE are the alternate interior angles.
Assume CF and AB as two lines which are intersected by the transversal DF.
In a similar way, ∠FCE and ∠DAE are the alternate interior angles.
Assume CF and AB are the two lines which are intersected by the transversal AC.
Therefore, CF ∥ AB
So, CF ∥ BD
and CF = BD {since BD = AD, it is proved that CF = AD}
Thus, BDFC forms a parallelogram.
By the properties of a parallelogram, we can write
BC ∥ DF
and BC = DF
BC ∥ DE
and DE = (1/2 * BC).
Hence, the midpoint theorem is proved.
Converse Midpoint Theorum
if a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side
Hope it helps ☺️❣️