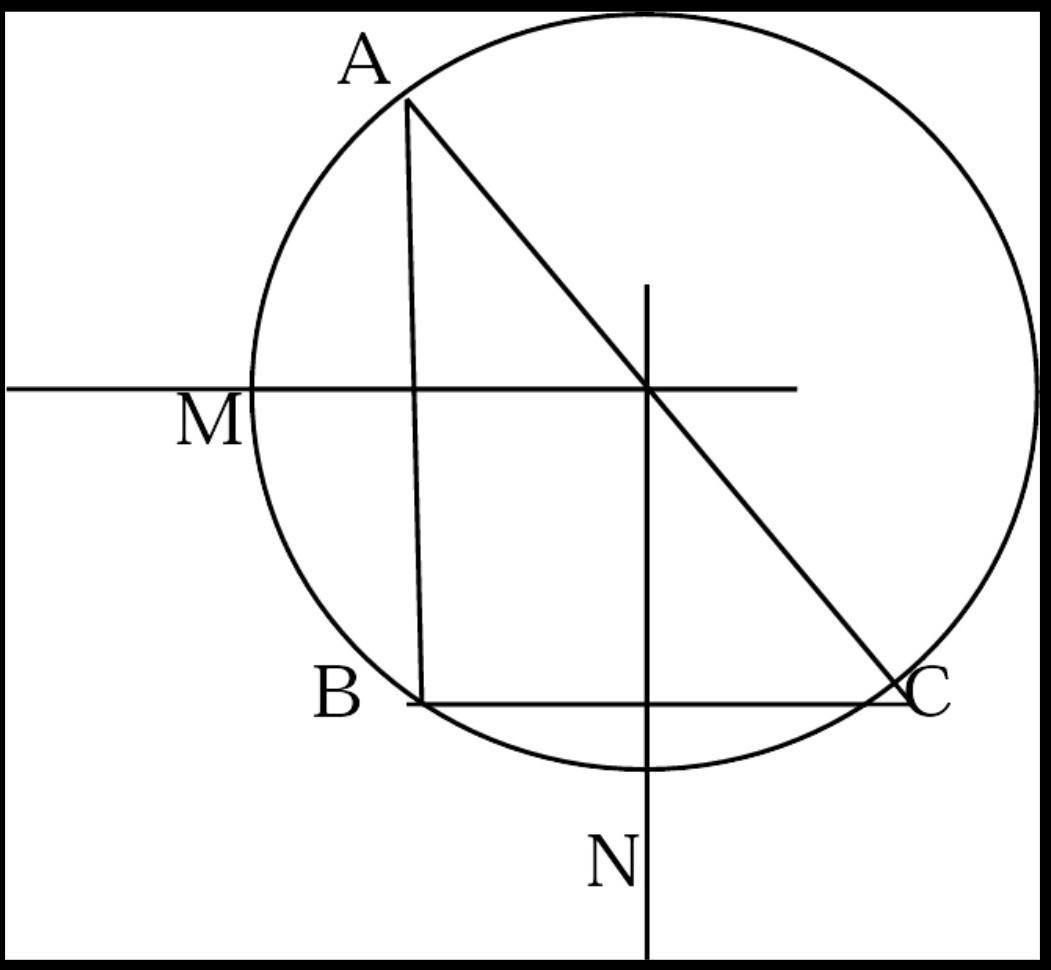
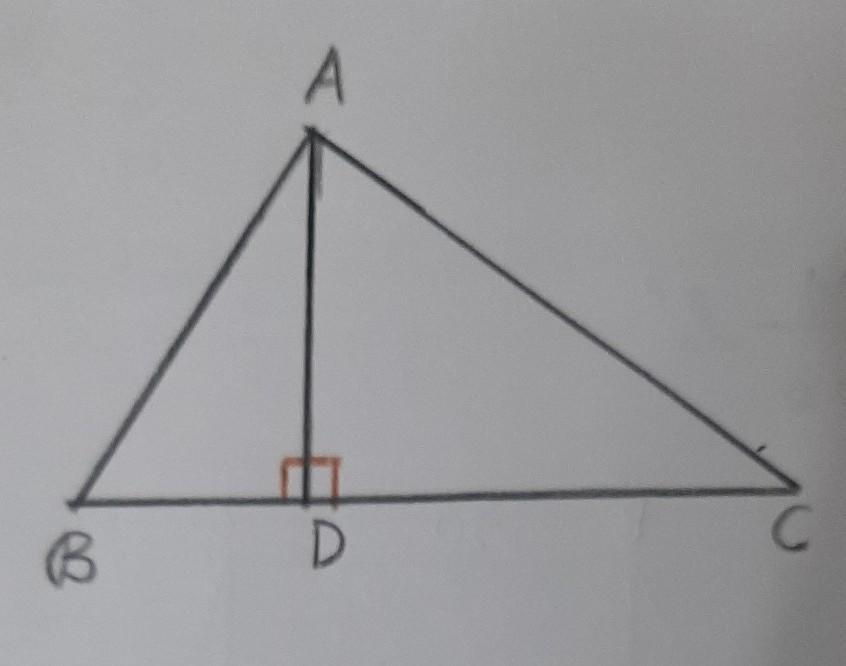
(ii) In A ABC, seg AD perpendicular seg BC. Prove : AB square+CDsquare=BDsquare+ ACsquare
Answers 2
Question :- In triangle ABC, segment AD is perpendicular to BC. Prove that
[tex]\rm \: {AB}^{2} + {CD}^{2} = {BD}^{2} + {AC}^{2} \\ [/tex]
[tex]\large\underline{\sf{Solution-}}[/tex]
As it is given that
[tex]\rm \: AD \: \perp \: BC \\ [/tex]
[tex]\rm\implies \angle\:ADB \: = \: \angle ADC \: = \: 90 \degree \\ [/tex]
Now, in right angle triangle ADB
By using Pythagoras Theorem, we have
[tex]\rm \: {AB}^{2} = {AD}^{2} + {BD}^{2} \\ [/tex]
[tex]\rm\implies \: {AD}^{2} = {AB}^{2} - {BD}^{2} - - - (1) \\ [/tex]
Now, in right angle triangle ADC
By using Pythagoras Theorem, we have
[tex]\rm \: {AC}^{2} = {AD}^{2} + {CD}^{2} \\ [/tex]
[tex]\rm\implies \: {AD}^{2} = {AC}^{2} - {CD}^{2} - - - (2) \\ [/tex]
From equation (1) and (2), we get
[tex]\rm \: {AB}^{2} - {BD}^{2} = {AC}^{2} - {CD}^{2} \\ [/tex]
[tex]\rm\implies \:\boxed{ \rm{ \: {AB}^{2} + {CD}^{2} = {BD}^{2} + {AC}^{2} \: \: }} \\ [/tex]
Hence, Proved
[tex]\rule{190pt}{2pt}[/tex]
Additional Information :-
1. Pythagoras Theorem :-
This theorem states that : In a right-angled triangle, the square of the longest side is equal to sum of the squares of remaining sides.
2. Converse of Pythagoras Theorem :-
This theorem states that : If the square of the longest side is equal to sum of the squares of remaining two sides, angle opposite to longest side is right angle.
3. Area Ratio Theorem :-
This theorem states that :- The ratio of the area of two similar triangles is equal to the ratio of the squares of corresponding sides.
4. Basic Proportionality Theorem,
This theorem states that : - If a line is drawn parallel to one side of a triangle, intersects the other two lines in distinct points, then the other two sides are divided in the same ratio.
-
Author:
shadybird
-
Rate an answer:
1
by cancelling AD from right hand side we get BD square -CD square
and interchanging the position of negative segments we can prace this proof

-
Author:
coalburton
-
Rate an answer:
9