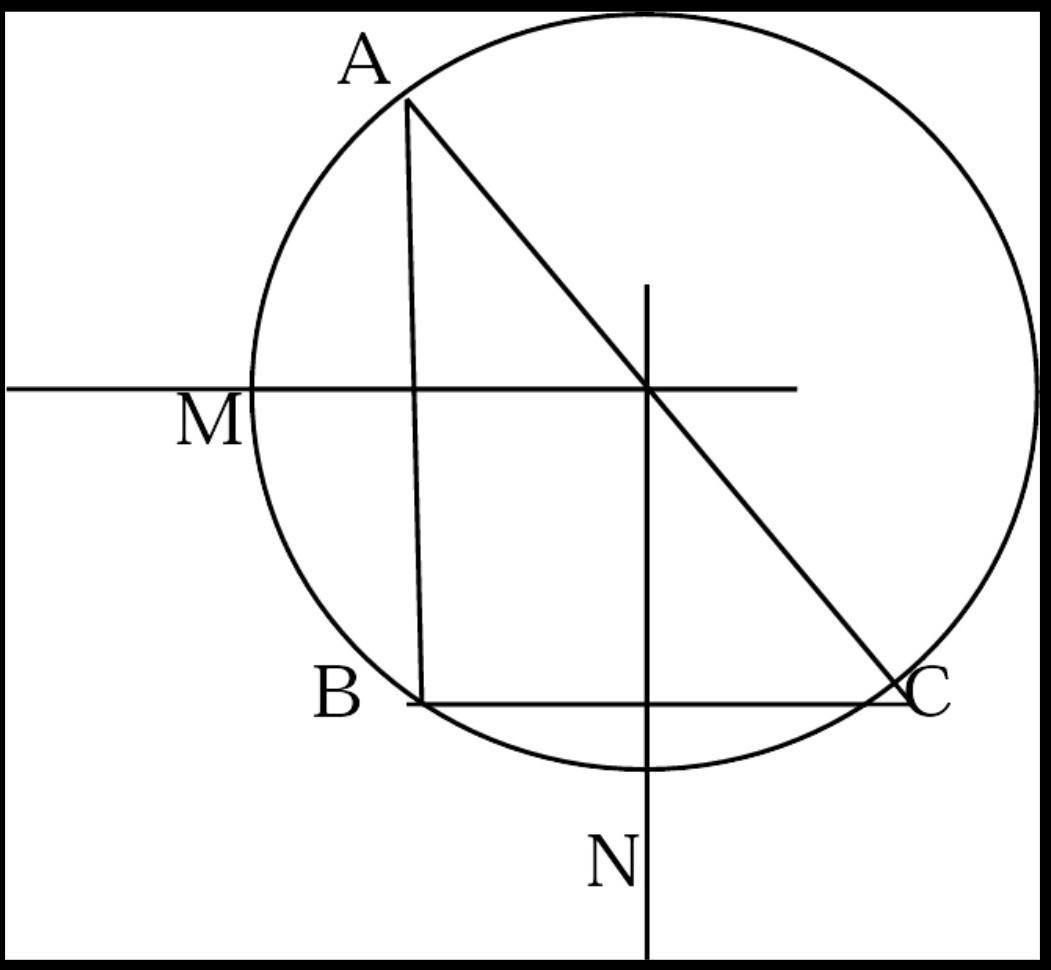
Read the text below and answer the following questions: As Class IX – C’s teacher Mrs. Rashmi entered in the class, she told students to do some practice on circles chapter. She draws two – lines AB and BC such that AB = 8 cm and BC = 6 cm. She told the children to make this shape in their notebook and draw a circle passing through A, B and C with center O. The children drew AB and BC as per figure. They also constructed perpendicular bisectors OM and ON for lines AB and BC. i) What will you call the line AOC? ii) What is the measure of ∠ABC? iii) What will you call the area AMB? iv) What is the radius of the circle? v) What is the area of ΔABC?
Answers 2
Answer:
- DIAMETER
- 90°
- ARC
- AO AND OC
- 8^2+6^2=64+36=√100=10^2
- SO THE AREA OF ABC IS
- √12(4)(6)(2)
- √2*3*2*2*2*2*3*2
- 2*2*2*3
- 24cm^2
Step-by-step explanation:
HOPE HELPFUL-
Author:
patrick685
-
Rate an answer:
15
Answer:
- The line AOC is diameter of the circle with centre O.
- Angle ABC is right angle i.e. 90⁰ .
- Area AMB is arc of circle with centre O.
- The radius of circle with centre O is 5 units .
- The area of ∆ ABC is 24 sq. units.
Step-by-step explanation:
PART 1 :
- Line AOC is a straight line which passes through centre and intersect the circle at two points A and C.
- Hence, it is diameter of the circle with centre O.
PART 2 :
- The inscribed angle theorem states that: " An angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. "
- Angle AOC subtends 180⁰ at the centre of the circle and angle ABC is half of the angle subtended at the centre.
- Angle ABC is :
[tex] \frac{ {180}^{0} }{2} = {90}^{0} [/tex]
- Hence, Angle ABC is a right angle.
PART 3 :
- Area AMB is the arc of the circle with centre o.
PART 4:
- From geometry of the figure ABC, it is evident that ∆ABC is a right angled triangle with right angle at B.
- By Pythagoras theorem:
(AB)² + (BC)² = (AC)²
- Given that AB = 8 cm and BC = 6 cm.
- This gives AC =
[tex] \: \: \: \: \: \: \: \: = \sqrt{ {8}^{2} + {6}^{2} } \\ \: \: \: \: \: \: \: = \sqrt{ 64 + 36 } \\ = \sqrt{100} \\ = 10 \: cm[/tex]
- AC is the diameter of the circle with centre O. Radius of the circle is
[tex] \frac{10}{2} = 5 \: cm[/tex]
PART 5 :
- ∆ ABC is a right angled triangle with right angle at B.
- Base of triangle = 6 cm
- Height of triangle = 8 cm
- Area of triangle is given by :
[tex] \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: = \frac{1}{2} \times base \times height \\ = \frac{1}{2} \times 8 \times 6 \\ = 24 \: sq \: cm[/tex]
Hence, area of ∆ ABC is 24 sq. cm .
-
Author:
lexiehorn
-
Rate an answer:
2
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years