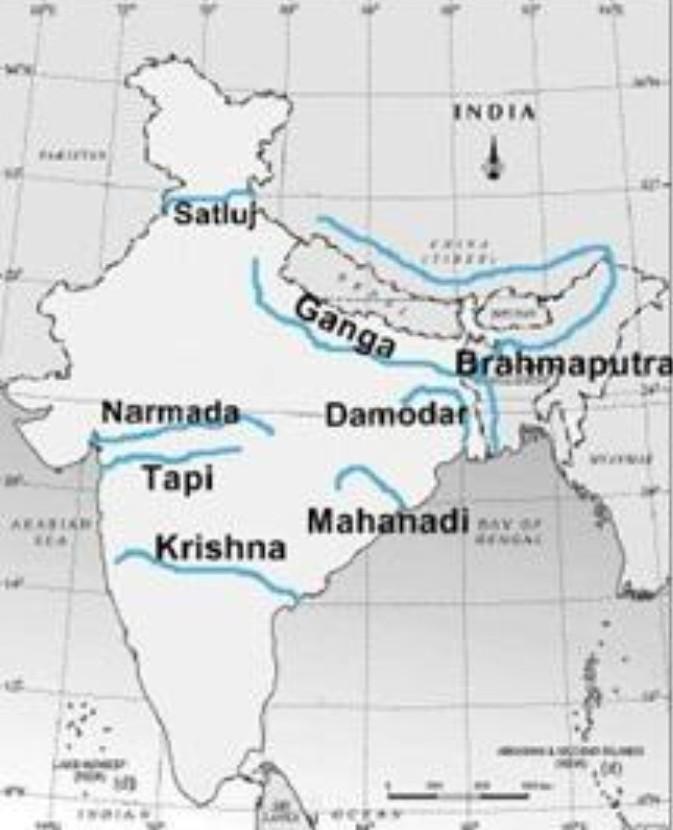
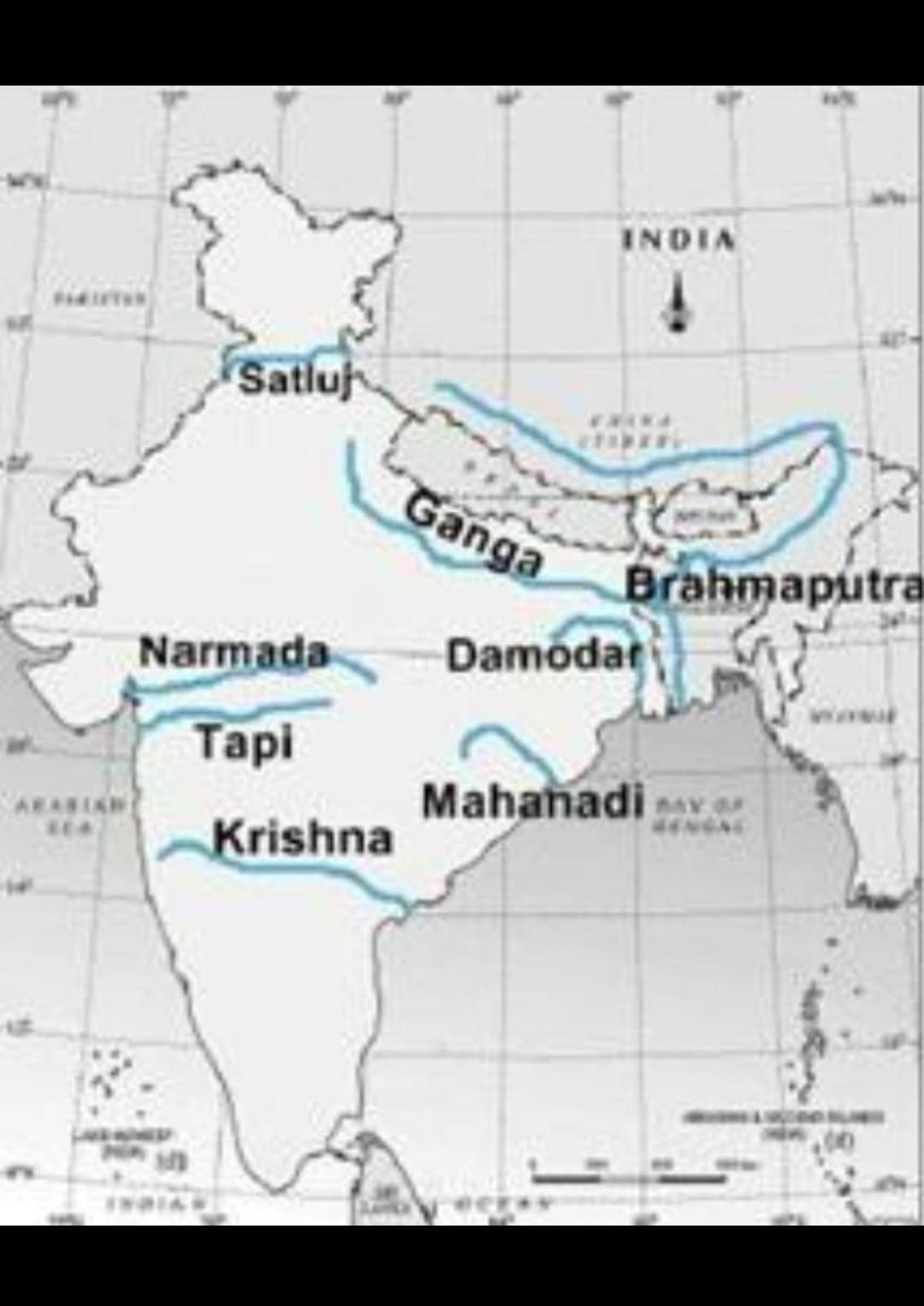
on the outline map of India Mark and label the following rivers Ganga Satluj Damodar Krishna Narmada Tapi Mahanadi and BrahmaputraDON'T SPAM !
-
Subject:
Political Science -
Author:
dixie -
Created:
1 year ago
Answers 2
Answer:
here is your answer dear :)
-
Author:
baldomerotgbf
-
Rate an answer:
19
Answer:
They all are 7 nice rivers of India
I know that u don't remember me
but I am jia
radhe radhe
-
Author:
braden619
-
Rate an answer:
8
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years
