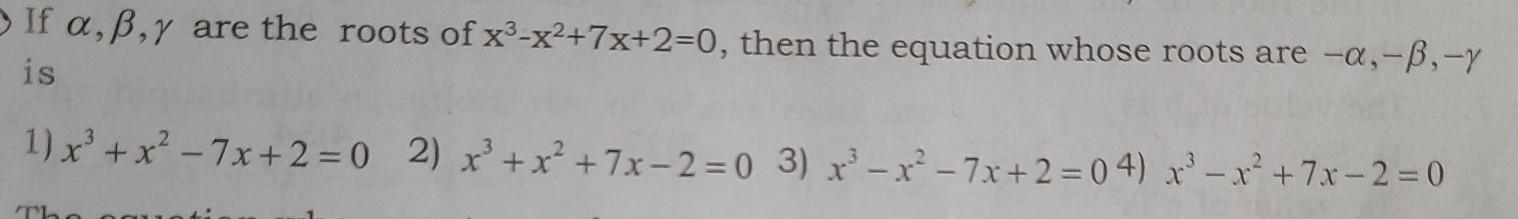two point charges having magnitude 5uc and 10 uc are separated by 10ohm where is electric potential zero on the line joining these two charges
-
Subject:
Physics -
Author:
xiomarazzua -
Created:
1 year ago
Answers 1
Answer:
you haven't written that we have to find what I just found force
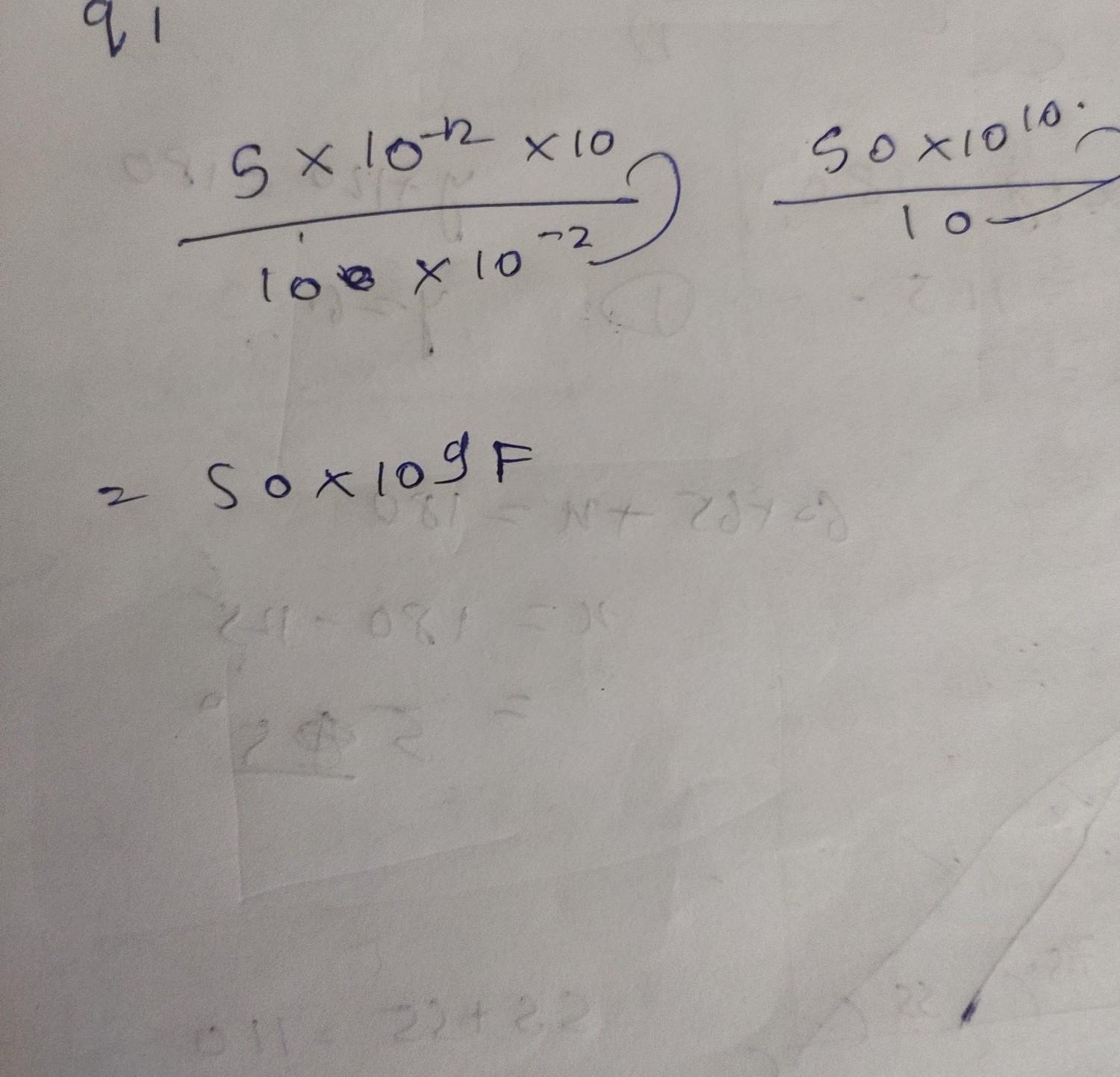
-
Author:
carleyberg
-
Rate an answer:
2
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years