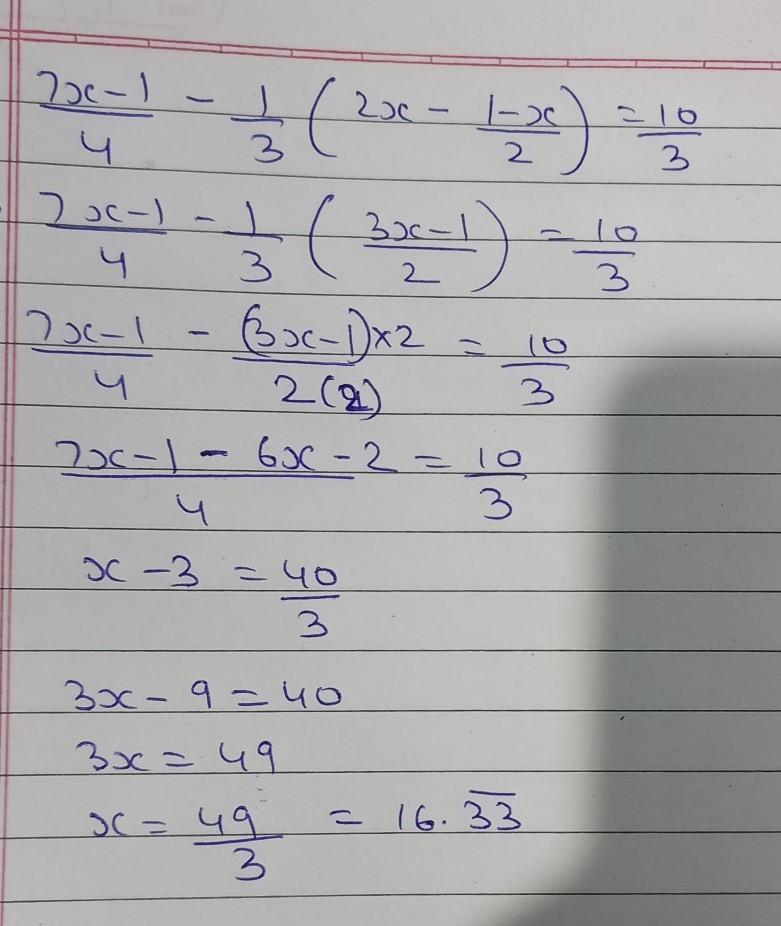Answer:
[tex]\qquad\qquad\qquad\boxed{ \sf{ \: \bf \:x = \dfrac{41}{11} \: \: }}\\ \\ [/tex]
Step-by-step explanation:
Given linear equation is
[tex]\sf \:\dfrac{7x - 1}{4} - \dfrac{1}{3}\left(2x - \dfrac{1 - x}{2}\right)= \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{7x - 1}{4} - \dfrac{1}{3}\left(\dfrac{4x - (1 - x)}{2}\right)= \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{7x - 1}{4} - \dfrac{1}{3}\left(\dfrac{4x - 1 + x}{2}\right)= \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{7x - 1}{4} - \dfrac{1}{3}\left(\dfrac{5x - 1}{2}\right)= \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{7x - 1}{4} -\dfrac{5x - 1}{6}= \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{3(7x - 1) - 2(5x - 1)}{12} = \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{21x - 3 - 10x + 2}{12} = \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{11x - 1}{12} = \dfrac{10}{3} \\ \\ [/tex]
[tex]\sf \:\dfrac{11x - 1}{4} = \dfrac{10}{1} \\ \\ [/tex]
[tex]\sf \:11x - 1 = 40 \\ \\ [/tex]
[tex]\sf \:11x = 40 + 1\\ \\ [/tex]
[tex]\sf \:11x = 41\\ \\ [/tex]
[tex]\sf\implies \bf \:x = \dfrac{41}{11} \\ \\ [/tex]