two concentric circle are of radii 4cm and 3cm find the length of the chord of the larger circle which touches the smaller circle
Answers 2
[tex]\large\underline{\sf{Solution-}}[/tex]
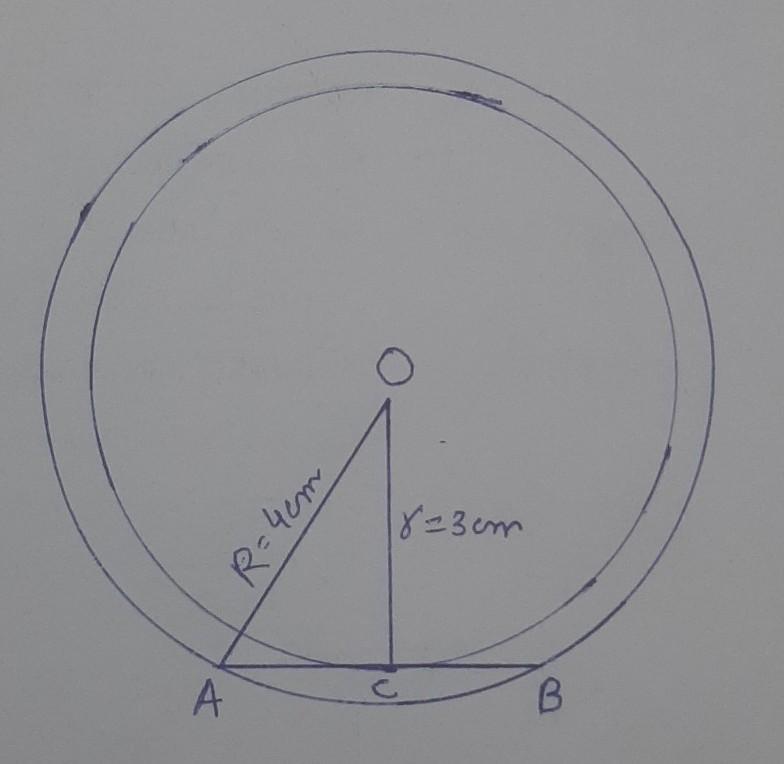
Let assume that C(O, r) and C(O, R) be two concentric circles with centre O and such that R = 4 cm and r = 3 cm.
Let further assume that AB be a chord of larger circle touches the small circle at C.
Construction :- Join OC
We know, radius and tangent are perpendicular to each other.
So, OC is perpendicular to AB.
Now, as OC is perpendicular to AB and we know, perpendicular drawn from centre bisects the chord.
So, AC = CB
Now, In right-angle triangle OAC
By using Pythagoras Theorem, we have
[tex]\sf \: {OA}^{2} = {OC}^{2} + {AC}^{2} \\ \\ [/tex]
[tex]\sf \: {R}^{2} = {r}^{2} + {AC}^{2} \\ \\ [/tex]
[tex]\sf \: {4}^{2} = {3}^{2} + {AC}^{2} \\ \\ [/tex]
[tex]\sf \: 16 = 9 + {AC}^{2} \\ \\ [/tex]
[tex]\sf \: {AC}^{2} = 16 - 9 \\ \\ [/tex]
[tex]\sf \: {AC}^{2} = 7 \\ \\ [/tex]
[tex]\bf\implies \:AC = \sqrt{7} \: cm \\ \\ [/tex]
Now,
[tex]\bf\implies \:AB = 2AC = 2\sqrt{7} \: cm \\ \\ [/tex]
-
Author:
chanceedot
-
Rate an answer:
8
Answer:
The length of the chord is [tex]2\sqrt{7}[/tex].
Step-by-step explanation:
According to the question , two concentric circle are of radii 4cm and 3cm.
We need to find the length of the chord of the larger circle which touches the smaller circle.
If we can draw the circles according to the question we can see that the joining line of the centre and the touching point is the radius of the small circle and also it is perpendicular to the chord and if we join any one side point of the chord with the centre than we can find that it is the radius of the larger circle.
So now we can see that it is a right angle triangle. length of half of the chord = [tex]\sqrt{4^{2} - 3^{2} } = \sqrt{7}[/tex]
So the length of the chord is [tex]2\sqrt{7}[/tex].
#SPJ3
-
Author:
pipershfz
-
Rate an answer:
2

