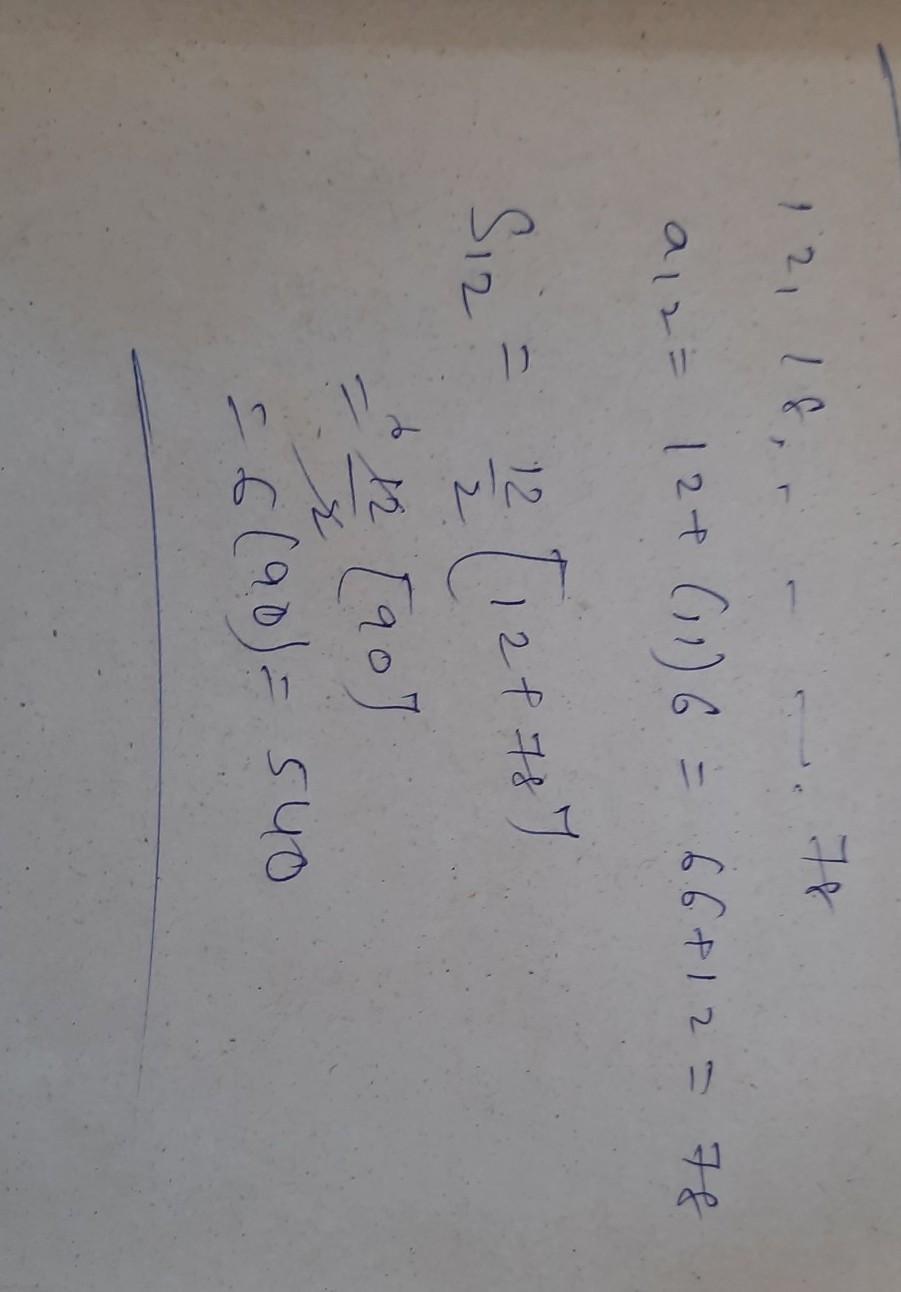If the median of the following data is 33 then, find the value of m: Class Frequency 0 - 15 1715 - 30 3530 - 45 4045 - 60 1860 - 75 m75 - 90 2
Answers 1
Answer:
good question you can try it by solving the question through the formula of median As given below -:L+(N/2-CF/F) *H try it and then checked answertry it and then check the answer-
Author:
maggie-moocamacho
-
Rate an answer:
10
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years