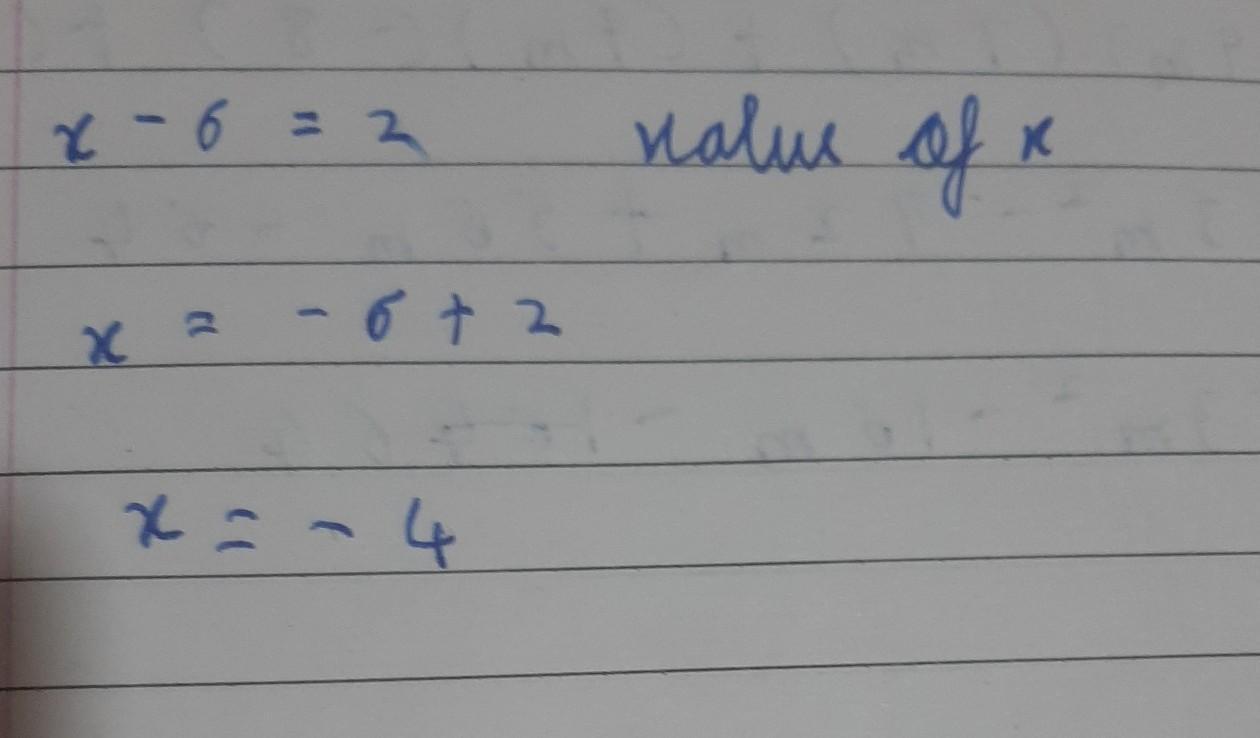A+b+c= 9 and ab+bc+ca= 26, than the value of a³+b³+c³= ?

Answers 1

EXPLANATION.

⇒ a + b + c = 9. - - - - - (1).

⇒ ab + bc + ca = 26. - - - - - (2).

As we know that,

Formula of :

⇒ (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.

Using this formula in this question, we get.

⇒ (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca.

⇒ (a + b + c)² = a² + b² + c² + 2(ab + bc + ca).

Put the values in the equation, we get.

⇒ (9)² = a² + b² + c² + 2(26).

⇒ 81 = a² + b² + c² + 52.

⇒ a² + b² + c² = 81 - 52.

⇒ a² + b² + c² = 29. - - - - - (3).

As we know that,

Formula of :

⇒ x³ + y³ + z³ - 3xyz = (x + y + z)(x² + y² + z² - xy - yz - zx).

Using this formula in this question, we get.

⇒ a³ + b³ + c³ - 3abc = (a + b + c)[a² + b² + c² - ab - bc - ca].

⇒ a³ + b³ + c³ - 3abc = (a + b + c)[a² + b² + c² - (ab + bc + ca)].

Put the values in the equation, we get.

⇒ a³ + b³ + c³ - 3abc = (9)[29 - (26)].

⇒ a³ + b³ + c³ - 3abc = 9 x 3.

⇒ a³ + b³ + c³ - 3abc = 27.

Value of : a³ + b³ + c³ = 27 + 3abc.