If A , B and C are three points on a line and B is between A and C then prove that AC+BC = AB using Euclid 's axiom
-
Subject:
Math -
Author:
buttonskxmq -
Created:
1 year ago
Answers 2
Answer:
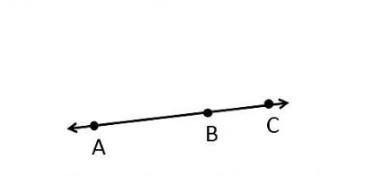
Given B is a point which lies on the line AC
∴ From Euclid's postulate,
AB+BC=AC
⇒AC−AB=BC
Hence, proved.
-
Author:
king1
-
Rate an answer:
15
Step-by-step explanation:
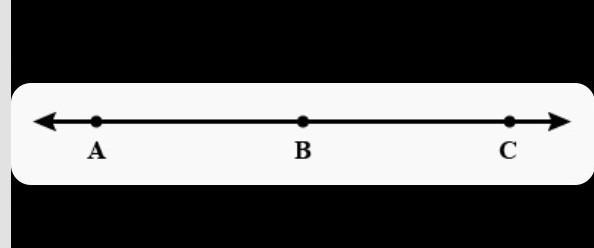
In the figure given above, AC coincides with AB+BC
From Euclid's Axiom 4 : Things which coincides with one another are equal to the one another.
So,we can write AB+BC=AC
-
Author:
angelblack
-
Rate an answer:
10
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years