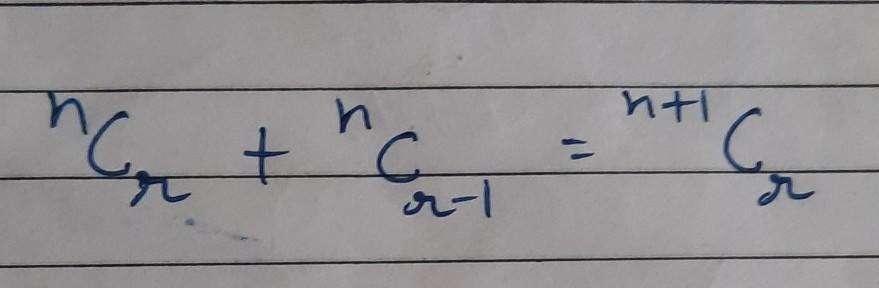find the value of x.
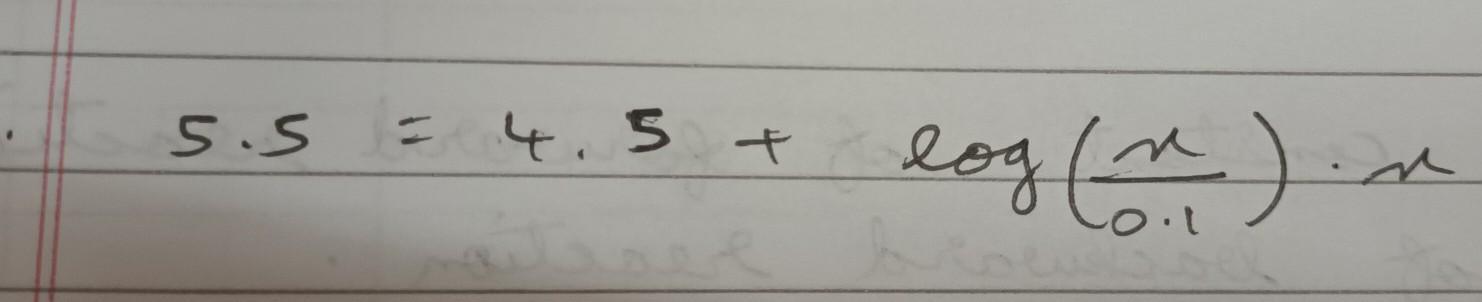
-
Subject:
Math -
Author:
savannacaldwell -
Created:
1 year ago
Answers 2
Step-by-step explanation:
I really don't know answer sorry dear friend
ykfxwzhpio
........,..........,..........
------------------------
-
Author:
orlando13
-
Rate an answer:
4
Is the question like this?
5.5=4.5+log(x/0.1)
Or
5.5=4.5+log(x/0.1)*x
My answer is as I wrote it in the first picture, and if it is not, I will repeat the solution
https://hi-static.z-dn.net/files/d51/d625f0e47a3081c8a40da46dfaedf61f.jpeg
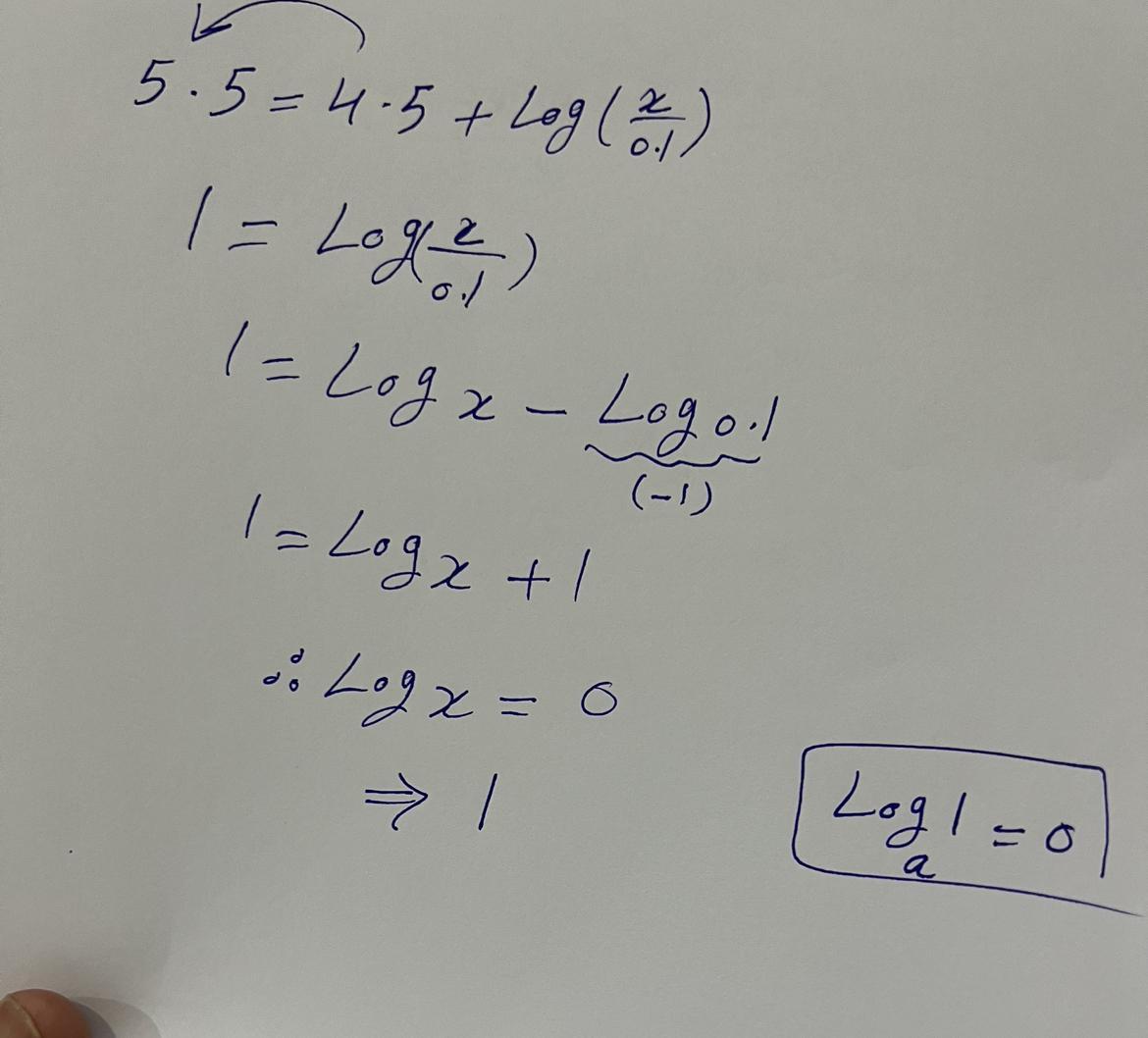
-
Author:
dawn
-
Rate an answer:
6
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years