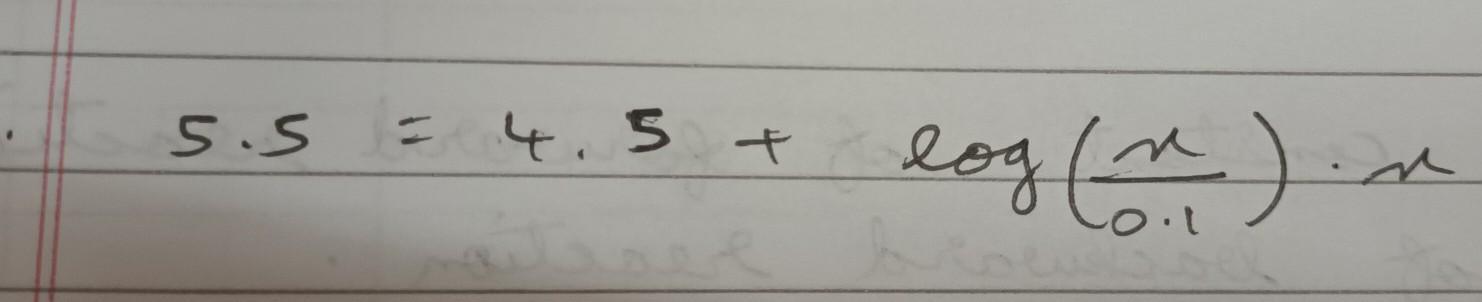Prove the following in attachment [tex] \binom{n}{r} + \binom{n}{r - 1 } = \binom{n + 1}{r} \\ [/tex]

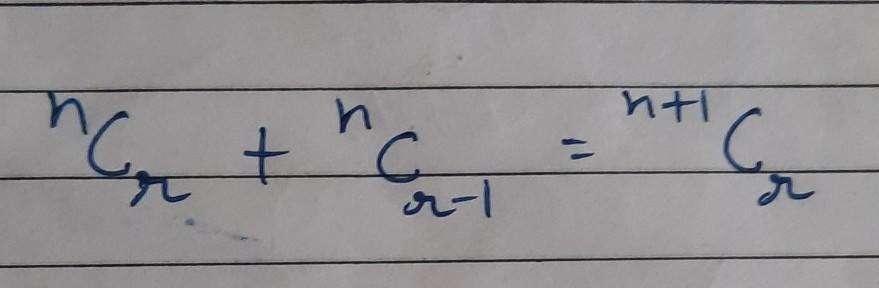
Answers 1

Answer:

Consider,

[tex]\sf \:\ ^nC_{r} + \ ^nC_{r - 1} \\ \\ [/tex]

We know,

[tex]\boxed{ \sf{ \:\ ^nC_{r} \: = \: \frac{n!}{r!(n - r)!} \: }} \\ \\ [/tex]

So, using this result, we get

[tex]\sf \: = \: \dfrac{n!}{r!(n - r)!} + \dfrac{n!}{(r - 1)!(n - r + 1)!} \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{n!}{r(r - 1)!(n - r)!} + \dfrac{n!}{(r - 1)!(n - r + 1)(n - r)!} \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{n!}{(r - 1)!(n - r)!}\left(\dfrac{1}{r} + \dfrac{1}{n - r + 1} \right) \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{n!}{(r - 1)!(n - r)!}\left( \dfrac{n - r + 1 + r}{r(n - r + 1)} \right) \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{n!}{(r - 1)!(n - r)!}\left( \dfrac{n+ 1}{r(n - r + 1)} \right) \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{(n + 1)n!}{r(r - 1)!(n - r + 1)(n - r)!} \\ \\ [/tex]

[tex]\sf \: = \: \dfrac{(n + 1)!}{r!(n + 1 - r)!} \\ \\ [/tex]

[tex]\sf \: = \: \ ^{n + 1}C_{r} \\ \\ [/tex]

Hence,

[tex]\sf\implies \bf \: \ ^nC_{r} + \ ^nC_{r - 1}= \: \ ^{n + 1}C_{r} \\ \\ [/tex]

[tex]\sf\implies \: \binom{n}{r} + \binom{n}{r - 1} = \binom{n + 1}{r} \\ \\ [/tex]

The Doctor is opreating the patient. change into passive

Answer the following What is History? answer

4 compounds from daily life

find the value of x.