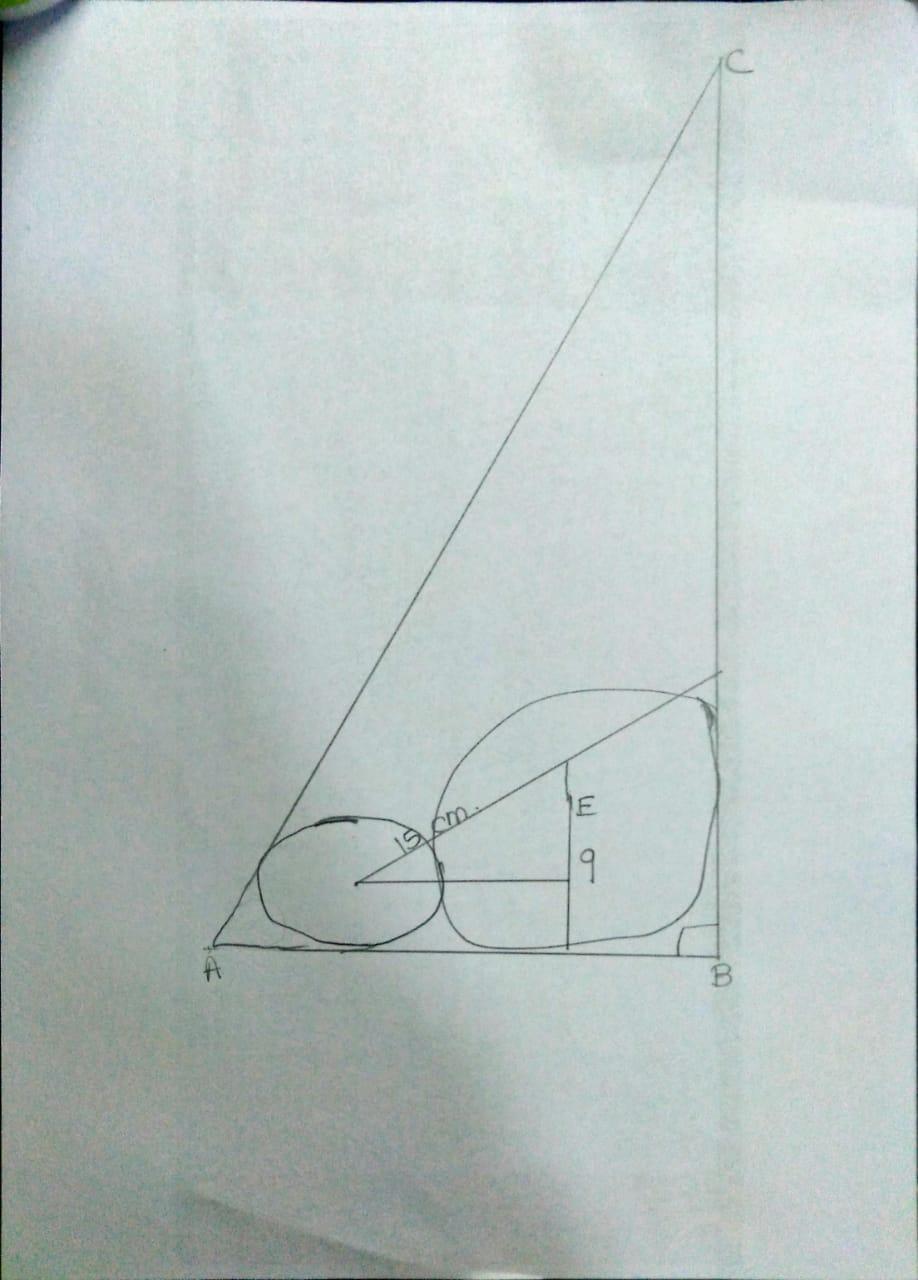
The circles are tangent to one another and each circle is tangent to the sides of the right triangle ABC with right angle ABC. If the larger circle has radius 12 and the smaller circle has radius 3, what is the area of the triangle?​ahhhh Mooooo! where were you? hru? @MonWenee (❁´◡`❁)​

The given sentence is:

Let us identify which part of speech each word in this sentence is.

✰ Subject (S) - The comedian

✰ Verb (V) - made

✰ Object (O) - us

✰ Complement (C) - happy

Therefore, the sentence follows a) SVOC sentence pattern.

The pattern of a sentence can be categorized into various categories. One such category is the S-V-O-C pattern (Subject-Verb-Object-Complement). Let us understand the different parts of speech in it:

✭ The subject: the doer or the performer of the action

✭ The verb: the action

✭ The object: recipient of the action

✭ Complement: a word that describes the subject or the object

Here are more SVOC sentences:

• Classes make me bored.
• I find it hilarious.
• The sun keeps us warm.

The answer to the given question is written below.

• The first option which is 'a) SVOC' is correct as it can be concluded form the given sentence.
• The second option which is 'b) SVCA' is incorrect as it cannot be concluded from the given sentence.
• The third option which is 'c) SVA' is incorrect as it cannot be concluded from the given sentence.
• The fourth option which is 'd) SVOC' is correct as it can be concluded from the given sentence.

Answer:

radius of the circle is 5 cm.

the coordinates of D is ( 4, -3 )

Step-by-step explanation:

Thanks☺☺

Answer:

a) D(4, -3)

b) radius = 5 units

Step-by-step explanation:

steps given in the image above.

Hope it helps!

Please mark as brainliest!! :)

Answer:

An old people's home is a place where old people live and are cared for when they are too old to look after themselves.

REASON:

There are old people who do not wish to be a burden to their kids and want to spend their golden years independently. This is why they choose to live in old age homes. They want to enjoy their life engaging in fun activities but at the same time having people to rely on to assist them with their needs. Parents can also be very selfless, wanting their kids to focus on their own lives instead of worrying about them all the time.

FACILITIES:

It depends on the ability of residents .Old age homes as good as 5 star Hotels are available if one is prepared to spend 30 to 50 lakks INR

Old age homes by Charitable Trusts offer minimum facilities with food

Some of the Govt Old Age homes provide Single room and minimum food and basic amenities

Answer:

There are various stages in human, life, including infancy, childhood, adolescence, adulthood, and old age. We all have to come and journey across these ages. However, our behaviour, attitude, temperaments and physical fitness are different in every stage. Also, not to forget that man is a social animal. He or she cannot stay in isolation. He needs to live in a family, with his friends in society. The entire world works smoothly on interdependence. Love, affection, and care are mutual, and they help a person live and not merely exist.

Due to the advent of urbanisation, modernisation and several other factors, the joint families have shattered. People are busy with their jobs, and they hardly have any time and interest to look after the older members of the family. Therefore, they leave their parents in old age homes. Also, many insensitive people, abandon their parents, and as a result of which various Non-governmental Organisations and governmental organisations rescue them and admit them to old age homes. Many people, who have no family to take care of, admit themselves to the old age home voluntarily.

An old age home is a shelter house where the people of older age dwell together with other older people when they have been abandoned by their family members or voluntarily admitted to it to combat loneliness during this crucial stage of life. The old-age house staff is in charge of feeding these senior citizens on time and taking care of their medical needs. They help them cope with the routine by cleaning their clothes and utensils and helping them live the last days of their life without isolation. Also, they conduct various recreational activities, to indulge them in and combat boring lifestyles. They entertain them so that they become happy and jolly. Also, the house inmates stay together, share their experiences and make good bonds with their friends.

Explanation:

I HOPE IT WILL HELPFUL FOR YOU

Answer:

Etiquette helps us know how to treat others. ... Etiquette makes people comfortable and at ease, it shows that we value and respect others. Etiquette promotes kindness, consideration, and humility. Etiquette gives the confidence to deal with different situations in life, it gives us life skills.