In a college, 200 students are randomly selected. 140 like tea, 120 like coffee and 80 like both tea and coffee. How many students neither like tea nor coffee?
Answers 2
200-140=60
200-120=80
80-60=140
140-80=60
Ans is 60
-
Author:
trampttcl
-
Rate an answer:
7
20 Students who neither like tea nor coffee.
n(A)+n(B)-n(A∩B)=20
Step-by-step explanation:
Given:
140 like tea, 120 like coffee, and 80 like both tea and coffee.
To find:
students who neither like tea nor coffee
Solution:
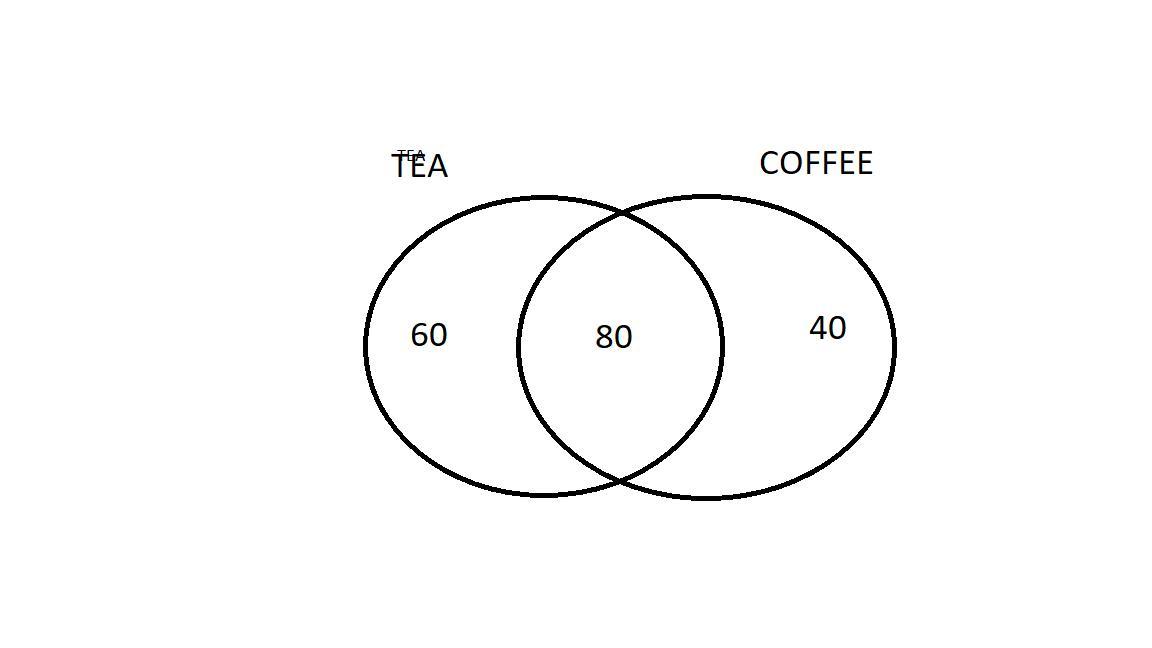
This is a Venn diagram representation.
Total number of students=200
Tea liking students =140
Coffee liking students =120
Both tea and coffee liking students n(A∩B)=80
To represent in the Venn diagram we need only tea liking and only coffee liking students.
Only Tea liking students can be obtained from the subtraction of tea liking students with Both Tea and Coffee liking students.
Only Tea liking students n(A)=140-80
n(A)=60
Only Coffee liking students can be obtained from the subtraction of Coffee liking students with Both Tea and Coffee liking students.
Only Coffee liking students n(B)=120-80
n(B)=40
We need to find the students neither like tea nor coffee which means they didn't take either tea or coffee which is given by,
⇒n(A)+n(B)-n(A∩B)
⇒60+40-80
⇒100-80
⇒ 20
Hence,
Students who neither like tea nor coffee are 20.
n(A)+n(B)-n(A∩B)=20
-
Author:
dawson432
-
Rate an answer:
1
If you know the answer add it here!
Other related questions that may help you
-
Author:
josie90
-
Author:
bernabéprice
-
Rate an answer:
12
-
Author:
narciso
-
Author:
myles874
-
Rate an answer:
9
-
Author:
pascual
-
Author:
admiralhoyp
-
Rate an answer:
9
-
Author:
muscleslama
-
Rate an answer:
9