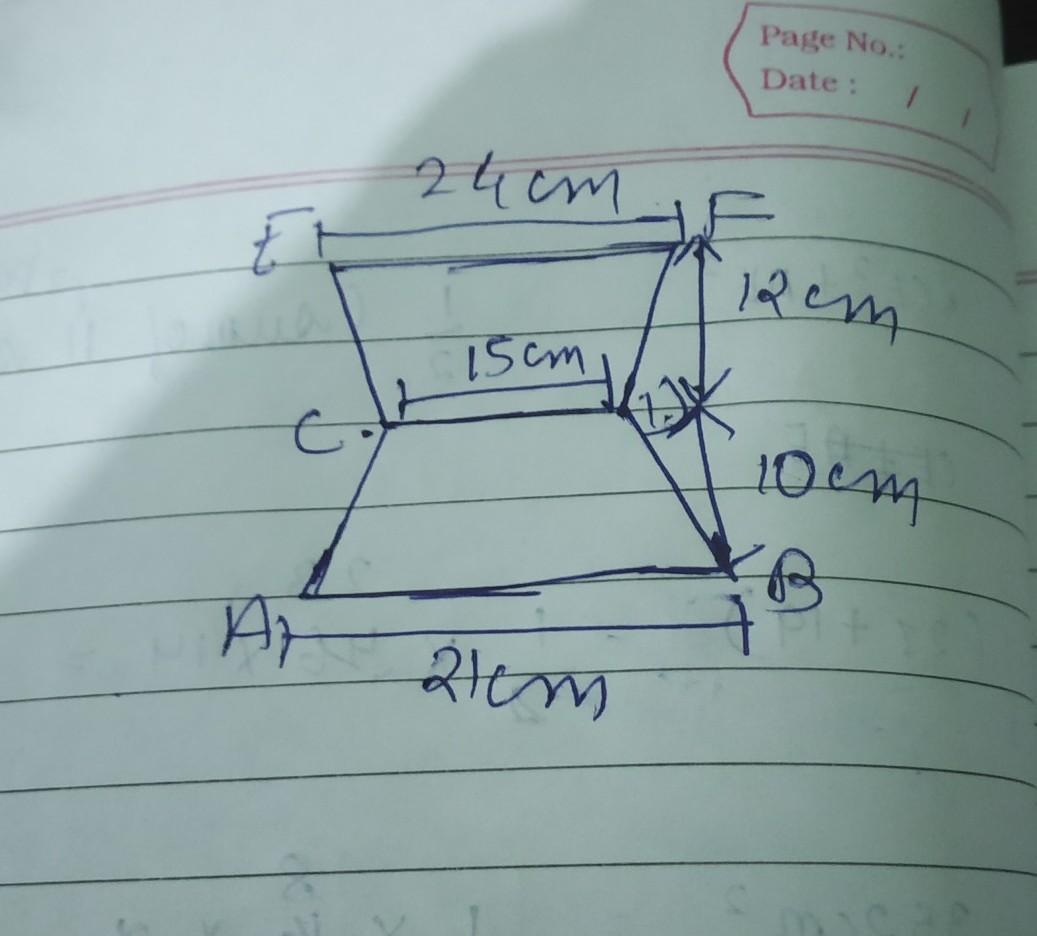
pease answer this question

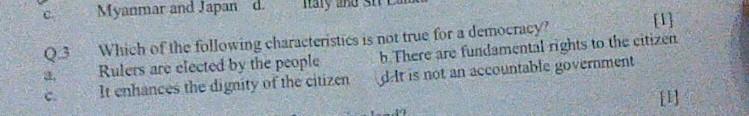
question img

Answers 1

Answer:

option d because democracy is one of the most accountable government in the world

Explanation:

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

a converts the data Passing between dissimilar networks answer​

Explanation:

A gateway is a network node used in telecommunications that connects two networks with different transmission protocols together. Gateways serve as an entry and exit point for a network as all data must pass through or communicate with the gateway prior to being routed.

find total area of figure ​
question img

55 this is the answer are u satisfied

Answer:

The total area of the figure = 444 cm²

Step-by-step explanation:

  • A quadrilateral in which a pair of opposite sides are parallel is called a trapezium.
  • If a and b are the length of two parallel sides of a trapezium, and h is the distance between the two parallel sides (height), then the area of the trapezium is given by,

[tex]A=\frac{h}{2} (a+b)[/tex]

Step 1:

The figure shows two trapezium EFDC and CDBA.

Total area of the given figure is the sum of area of the two trapeziums.

Step 2:

Trapezium EFDC has parallel sides and height as:

a = 24 cm (side EF)

b = 15 cm (side DC)

h = 12 cm

∴ Area of trapezium EFDC is,

[tex]A_{(EFDC)} =\frac{h}{2} (EF+DC)[/tex]

[tex]A_{(EFDC)} =\frac{12}{2} (24+15)[/tex]

[tex]A_{(EFDC)} = 234 cm^{2}[/tex]

Step 2:

Trapezium CDBA has parallel sides and height as:

b = 15 cm (side CD)

a = 21 cm (side BA)

h = 10 cm

∴ Area of trapezium CDBA is,

[tex]A_{(CDBA)} =\frac{h}{2} (CD+BA)[/tex]

[tex]A_{(CDBA)} =\frac{10}{2} (15+21)[/tex]

[tex]A_{(CDBA)} = 210 cm^{2}[/tex]

Step 3:

Total area of the given figure = area of trapezium EFDC + area of trapezium CDBA,

[tex]A_{(EFDBAC)} = A_{EFDC} +A_{CDBA}[/tex]

[tex]= 234 + 210[/tex]

[tex]= 444 cm^{2}[/tex]

[ssz / ycti /dmm] --> Music rejuvenates the mind. When music therapy is combined with other relaxation techniques based on guided imagery, it reduces depression, pain and anxiety. Fibromyalgia is a condition that causes pain, stiffness and tenderness of the muscles, tendons and joints. In such a condition music also improves sleep, Researchers used relaxation technique based on guided imagery and music therapy for treatment of patients ​

Answer:

mark me brilliant please and follow me

Explanation:

mark me brilliant

I need help what is 8 + 3

answer is 11. 8+3 is 11.

Other Political Science Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years