1) Describe Newton's 1st law of motion and Newton's 2nd law of motion.( anyone here )​

Answers 1

Explanation:

In the first law, an object will not change its motion unless a force acts on it.

In the second law, the force on an object is equal to its mass times its acceleration.

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

it was an outer room with one wall facing the open yard.it had a tiled roof with long supporting gables that rested on the beam over the wall1 Whose room is described here?where was this room located?2 what kind of roof did the room have?What purpose did it serve?​

Answer:

for this you should read question again

Explanation:

mark me the brainlist

सुशील के कपड़े उसके बदन में क्यों फस गए थे

Answer:

भाड़ में जाओ तुम्हें एक बच्चा मिलेगा

hhhhjhj kah v did sheywuw I qydk DS fnp se k

find mass if the force is 3n and the initial vel. is 4metre per seconds and final velocity is 10 metre per seconds and time is 10 seconds​

Answer:

hej36ji36je6i25j36i35k36kk3i17

அதாவது, பொதுவாக உங்கள் இரத்த சிவப்பணு (ஆர்.பி.சி) எண்ணிக்கை குறைவாக உள்ளது.

In the given figure (not drawn to scale), BA = BR and PQ is parallel to RS. Find x, y and z.
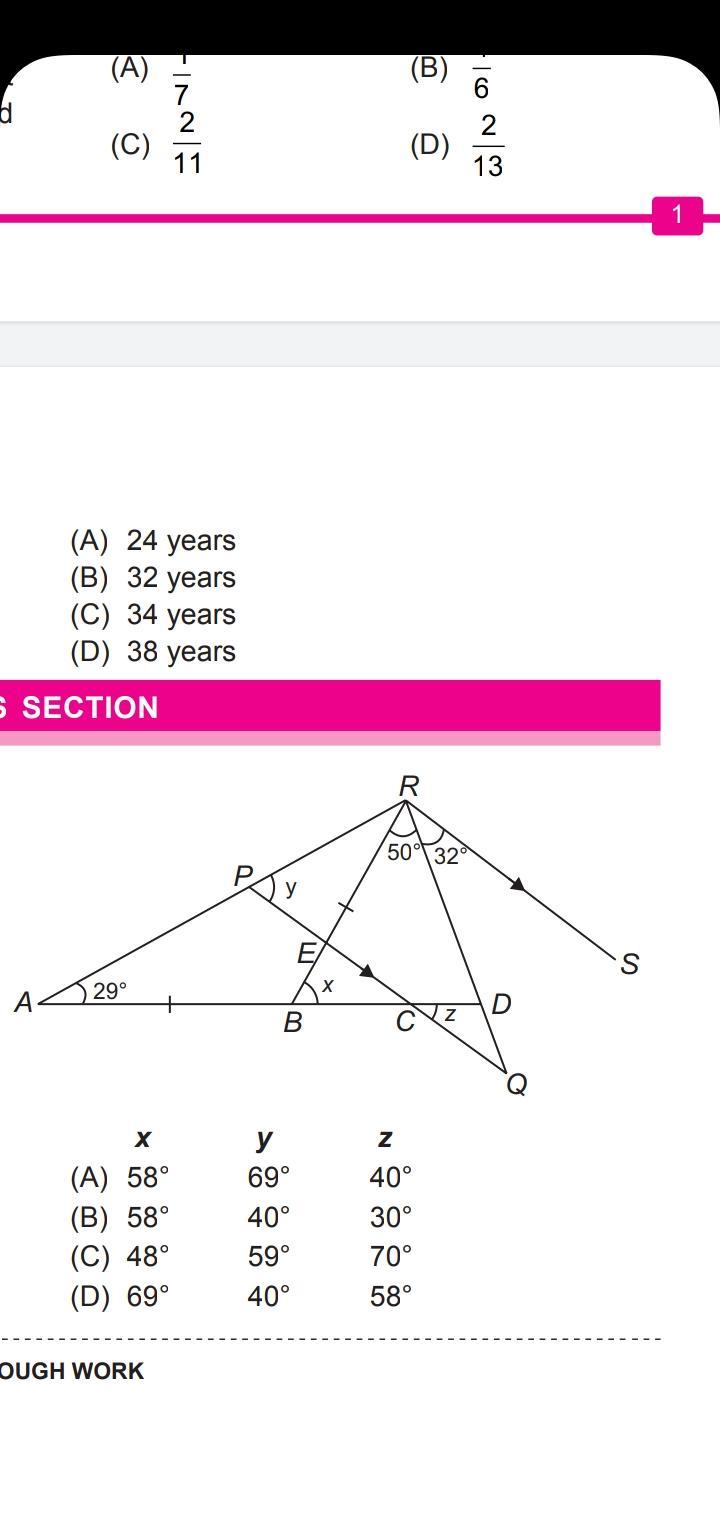
question img

Answer:

in triangle ABR

AB=BR ( Given)

so, angle BAR = BRA = 29 ° ------- i ( angles opp. to equal sides are equal)

Angle ABR = sum of angles of triangle - (29°+29°)

= 180°-58°

= 122° ----------- ii

now angle RBD = x

angle RBD + angle ABR = 180° ( linear pair)

x + 122°=180°

x = 58°

Now angle PRS + angle RPQ = 180° ( adjacent angles in a transversal )

Angle PRS = 50°+32°+angle BRA

Angle PRS = 50°+32°+29° ----- using i

Angle PRS = 111°

now ,

angle PRS + angle RPQ = 180°

y + 111°=180°

y = 69°

Considering RQ as the tranversal

angle QRS = angle PQR = 32° -------- iii

Now in triangle BRD

angle DBR = 58° (value of x)

angle BRD = 50° (given)

angle BDR = sum of angles of triangle - ( 50°+58°)

= 180°-108°

= 72°

now angle BDR + angle CDQ = 180° ( linera pair)

72° + angle CDQ = 180°

angle CDQ = 180°-72°

angle CDQ = 108°

Now in triangle CDQ

angle CDQ = 108°

angle CQD= 32° -------- using iii

angle QCD = z =sum of angles of triangle - (108+32)

= 180°-140°

Z = 40°

therefore the correct ✅option is A) x=58° , y= 69°, z = 40°

Other Physics Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years