The following Table is based on Curved Surfaces seperating two media:Answer both (i) and (ii) from Photo.​

1) compound

2) simple

3) complex

4) compound

5) compound

6) simple

please mark me brainlist

Answer:

The probability of getting not blue marbles will be 13/30

Answer:

Let box contains red marbles be R1, R2, R3, R4, R5, R6, R7, R8, R9, R10

Let box contains with white marbles be W1, W2, W3

Let box contains with blue marbles be B1, B2, B3, B4, B5, B6, B7, B8, B9, B10, B11, B12, B13, B14, B15, B16, B17

Let S be the sample space

n(S) =R1, R2, R3, R4, R5, R6, R7, R8, R9, R10, W1, W2, W3, B1, B2, B3, B4, B5, B6, B7, B8, B9, B10, B11, B12, B13, B14, B15, B16, B17

n(S) =30

Let A be the event that marble picked from box is not blue

P(A) =R1, R2, R3, R4, R5, R6, R7, R8, R9, R10, W1, W2, W3

P(A) =13

By definition of probability,

P(A) =n(A) /n(S)

13/30

Ans :- P(A) =13/30

Answer:

Radius of the sphere (r) is (b) 5 cm.

Volume of the half filled cylinder is (c) 1540 cm³.

Volume of sphere is (d) 523.8 cm³.

Volume of the complete filled cylinder is (c) 1.54 litre.

Surface area of the sphere is (a) 314.3 cm².

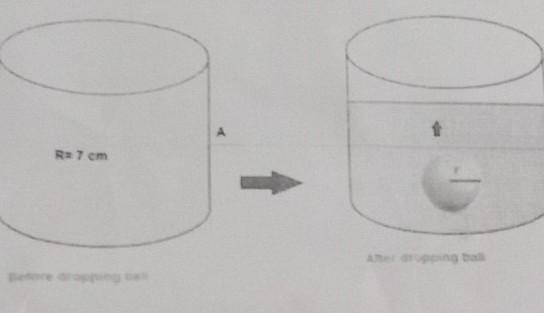
Given:

Radius of the cylinder (R) = 7 cm

Height of the cylinder (h) = 10 cm

To find:

Radius of the sphere (r).

Volume of the half filled cylinder.

Volume of sphere.

Volume of the complete filled cylinder.

Surface area of the sphere.

Explanation:

We have been given in the question that when a sphere is dropped in a half filled cylinder, the rise in water level is height (h') = 3.4 cm

Solution 1

From Archimedes Principle, we know that the volume of water that will rise in the cylinder, will be equal to the volume of the sphere .

Mathematically,

Volume of water rise  Volume of the sphere

                      πR²h'     4/3 π r³

             Hence,    

Substituting the values, we get

Therefore,

Solution 2

We have the given information, that the cylinder is filled up half.

Hence,      

Therefore,

Volume of the cylinder  πR²H          

Solution 3

We have calculated, radius of the sphere (r) = 5 cm

Therefore,

The volume of the sphere = 4/3 π r³

Substituting the values, we get  

Solution 4

Since, we have height of the full cylinder, that is h = 10 cm

and radius of the cylinder (R) = 7 cm

Therefore, the volume of the cylinder will be = πR²h  

Substituting the given values, we get

Given that,

1 litre = 1000 cm³  ;

Therefore,

1540 cm³ = 1.54 L

Solution 5

We know the surface area of the sphere = 4πr²

where, radius of the sphere r = 5 cm

Hence,

Surface area

Final answer:

Hence,

Radius of the sphere (r) is (b) 5 cm.

Volume of the half filled cylinder is (c) 1540 cm³.

Volume of sphere is (d) 523.8 cm³.

Volume of the complete filled cylinder is (c) 1.54 litre.

Surface area of the sphere is (a) 314.3 cm².

Step-by-step explanation:

let us consider the height of the tower 'h'

we know that 'h'= AC tan 30 degree = BC tan 30 degree

We know that AC=BC [∵ radius of circle]

Hence, we can say that △ABC is an isosceles triangle with AC=BC.

So, ∠ABC=∠BAC ...(2)

But ∠ACB=60

∘

[given]

⇒∠ABC+∠BAC+∠ACB=180

∘

⇒∠ABC+∠ABC+60

∘

=180

∘

[from (2)]

⇒2×∠ABC=120

∘

∴∠ABC=∠BAC=60

∘

Hence △ABC is an equilateral triangle.

∴AB=BC=CA=a ...(3)

∴h=atan30

∘

[form equation (1)]

=

3

a

Step-by-step explanation:

Solution

verified

Verified by Toppr

Correct option is C)

Let us consider the height of the tower as h

We know that, h=ACtan30

∘

=BCtan30

∘

...(1)

We know that AC=BC [∵ radius of circle]

Hence, we can say that △ABC is an isosceles triangle with AC=BC.

So, ∠ABC=∠BAC ...(2)

But ∠ACB=60

∘

[given]

⇒∠ABC+∠BAC+∠ACB=180

∘

⇒∠ABC+∠ABC+60

∘

=180

∘

[from (2)]

⇒2×∠ABC=120

∘

∴∠ABC=∠BAC=60

∘

Hence △ABC is an equilateral triangle.

∴AB=BC=CA=a ...(3)

∴h=atan30

∘

[form equation (1)]

=

3

a