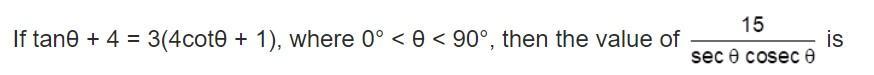find mean and variance of 5x-3​

Step-by-step explanation:

Answer:

\begin{gathered}\qquad \:\boxed{\begin{aligned}& \qquad \:\sf \: Price \: of \: notebook=Rs \: 45 \qquad \: \\ \\& \qquad \:\sf \:Price \: of \:instrument \: box =Rs \: 75 \end{aligned}} \qquad \\ \\ \end{gathered}

Priceofnotebook=Rs45

Priceofinstrumentbox=Rs75

Step-by-step explanation:

Let assume that

Price of one notebook be Rs x

Price of one instrument box be Rs y

According to statement, price of 1 notebook and one instrument box is Rs 120.

It means,

\begin{gathered}\sf\implies x + y = 120 \: \: \: - - - (1) \\ \\ \end{gathered}

⟹x+y=120−−−(1)

Further given that, the price of 3 notebooks and one instrument box is Rs 210.

\begin{gathered}\sf\implies 3x + y = 210 \: \: \: - - - (2) \\ \\ \end{gathered}

⟹3x+y=210−−−(2)

On Subtracting equation (1) from (2), we get

\begin{gathered}\sf \:2x = 90 \\ \\ \end{gathered}

2x=90

\begin{gathered}\sf\implies \bf \:x = 45 \\ \\ \end{gathered}

⟹x=45

On substituting the value of x in equation (1), we get

\begin{gathered}\sf \:45 + y = 120 \\ \\ \end{gathered}

45+y=120

\begin{gathered}\sf \:y = 120 - 45\\ \\ \end{gathered}

y=120−45

\begin{gathered}\sf\implies \bf \:y = 75\\ \\ \end{gathered}

⟹y=75

Hence,

\begin{gathered}\sf\implies \:\boxed{\begin{aligned}& \qquad \:\bf \: Price \: of \: notebook=Rs \: 45 \qquad \: \\ \\& \qquad \:\bf \:Price \: of \:instrument \: box =Rs \: 75 \end{aligned}} \qquad \\ \\ \end{gathered}

⟹

Priceofnotebook=Rs45

Priceofinstrumentbox=Rs75

\rule{190pt}{2pt}

Additional Information

\begin{gathered}\begin{gathered}\: \: \: \: \: \: \begin{gathered}\begin{gathered} \footnotesize{\boxed{ \begin{array}{cc} \small\underline{\frak{\pmb{{More \: identities}}}} \\ \\ \bigstar \: \bf{ {(x + y)}^{2} = {x}^{2} + 2xy + {y}^{2} }\:\\ \\ \bigstar \: \bf{ {(x - y)}^{2} = {x}^{2} - 2xy + {y}^{2} }\:\\ \\ \bigstar \: \bf{ {x}^{2} - {y}^{2} = (x + y)(x - y)}\:\\ \\ \bigstar \: \bf{ {(x + y)}^{2} - {(x - y)}^{2} = 4xy}\:\\ \\ \bigstar \: \bf{ {(x + y)}^{2} + {(x - y)}^{2} = 2( {x}^{2} + {y}^{2})}\:\\ \\ \bigstar \: \bf{ {(x + y)}^{3} = {x}^{3} + {y}^{3} + 3xy(x + y)}\:\\ \\ \bigstar \: \bf{ {(x - y)}^{3} = {x}^{3} - {y}^{3} - 3xy(x - y) }\:\\ \\ \bigstar \: \bf{ {x}^{3} + {y}^{3} = (x + y)( {x}^{2} - xy + {y}^{2} )}\: \end{array} }}\end{gathered}\end{gathered}\end{gathered}\end{gathered}

Moreidentities

Moreidentities

★(x+y)

2

=x

2

+2xy+y

2

★(x−y)

2

=x

2

−2xy+y

2

★x

2

−y

2

=(x+y)(x−y)

★(x+y)

2

−(x−y)

2

=4xy

★(x+y)

2

+(x−y)

2

=2(x

2

+y

2

)

★(x+y)

3

=x

3

+y

3

+3xy(x+y)

★(x−y)

3

=x

3

−y

3

−3xy(x−y)

★x

3

+y

3

=(x+y)(x

2

−xy+y

2

)