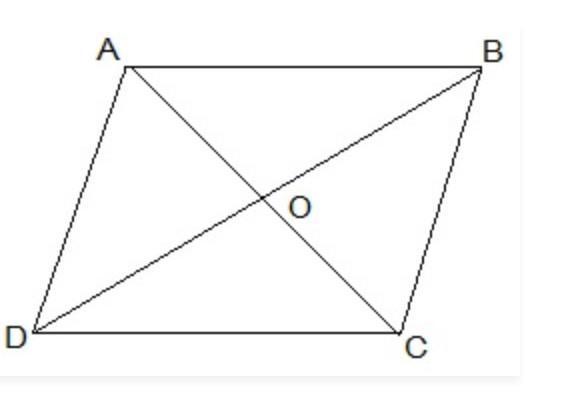
Show that the diagonals of a parallelogram divide it into four triangles of equal areaschii ..... kl walii baat naraj too nhii ho ne
Answers 2
To prove:- ar(△AOB)=ar(△BOC)=ar(△COD)=ar(△AOD)
Proof:-
Let ABCD be a parallelogram with diagonals AC and BD
intersecting at O. Since the diagonals of a parallelogram bisect each other at the point of intersection.
Therefore,
AO=OC and BO=OD
We know that the median of a triangle divides it into two equal parts.
Now,
In △ABC,
∵BO is median.
ar(△AOB)=ar(△BOC).....(1)
In △BCD,
∵CO is median.
ar(△BOC)=ar(△COD).....(2)
In △ACD,
∵DO is median.
ar(△AOD)=ar(△COD).....(3)
From equation (1),(2)&(3), we get
ar(△AOB)=ar(△BOC)=ar(△COD)=ar(△AOD)
Hence proved.
-
Author:
harry
-
Rate an answer:
5
Answer:
O is the mid point of AC and BD. (diagonals of bisect each other)
In ΔABC, BO is the median.
∴ar(AOB) = ar(BOC) — (i)
also,
In ΔBCD, CO is the median.
∴ar(BOC) = ar(COD) — (ii)
In ΔACD, OD is the median.
∴ar(AOD) = ar(COD) — (iii)
In ΔABD, AO is the median.
∴ar(AOD) = ar(AOB) — (iv)
From equations (i), (ii), (iii) and (iv), we get,
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
Hence, we get, the diagonals of a parallelogram divide it into four triangles of equal area.
Step-by-step explanation:
hmm .....
nhii yrrr
smja rhe sii me bss
-
Author:
chance40
-
Rate an answer:
13
