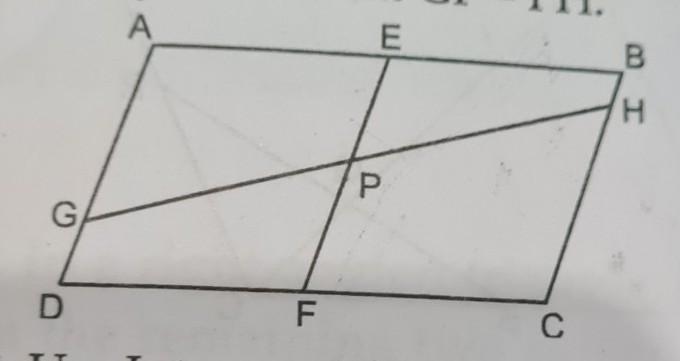
15. ABCD is a parallelogram. E and F are the mid- points of AB and CD respectively. GH is any line that intersects AD, EF and BC in G, P and H respectively. Prove that GP= PH. [Hint: Use Intercept Theorem on AD || EF || BC.]
Answers 2
Answer:
15. ABCD is a parallelogram. E and F are the mid- points of AB and CD respectively. GH is any line that intersects AD, EF and BC in G, P and H respectively. Prove that GP= PH. [Hint: Use Intercept Theorem on AD || EF || BC.]
-
Author:
gooseavila
-
Rate an answer:
10
Answer:
Since E and F are mid-points AB and CD respectively.
∴AE=BE=
2
1
AB and CF=DF=
2
1
CD
But, AB=CD
∴
2
1
AB=
2
1
CD⇒BE=CF
Also, BE∥CF [∵AB∥CD]
∴ BEFC is a parallelogram.
⇒BC∥EF and BE=PH ...(i)
Now, BC∥EF
⇒AD∥EF [∵BC∥AD as ABCD is a ∥
gm
]
⇒AEFD is a parallelogram
⇒AE=GP ...(ii)
But, E is the mid-point of AB.
∴AE=BE
⇒GP=PH [Using (i) and (ii)]
Step-by-step explanation:
please mark me as a brainly
-
Author:
lowery
-
Rate an answer:
11
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years
