Answers 2
Answer:
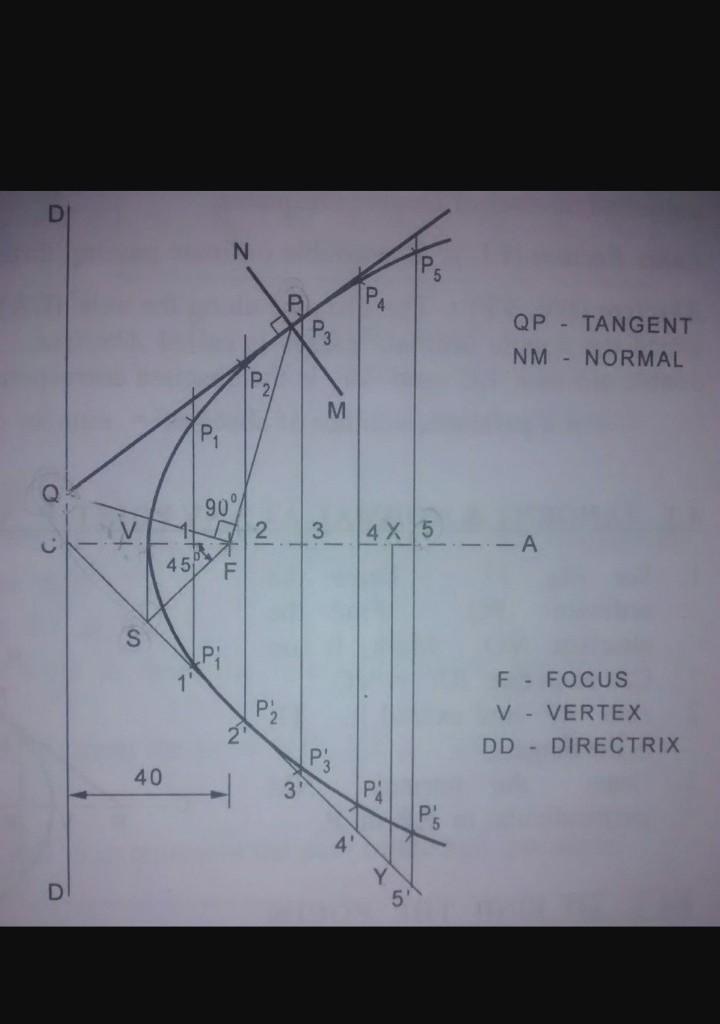
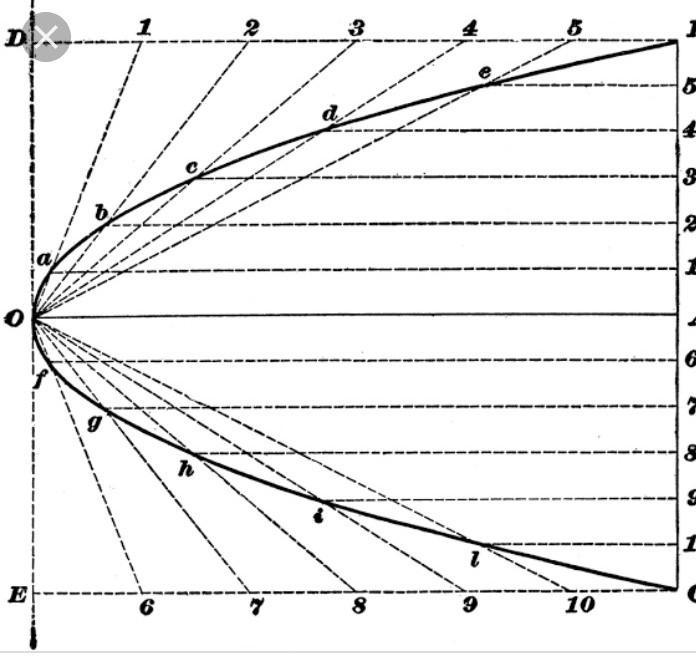
. In figure 1, point A is constructed as the focus and line BD as the directrix.
Figure 1
2. Next, point C is randomly constructed on segment BD. Through C, a line perpendicular to segment BD is constructed. Point C must be constructed randomly to insure that the perpendicular line can move along segment BD.
Figure 2
3. Now, segment AC is constructed with its perpendicular bisector line FE.
Figure 3
To understand this step, it might be helpful to keep in mind the definition of the parabola and to think about its vertex. Its vertex will be located at point E halfway between line BD and point A when the perpendicular is in line with point A. (See figure 4.)
Figure 4
4. Next, select point F, choose “trace” from the Display Menu and then drag point C back and forth along segment BD to draw the parabola as shown in figure 5. (The more you “trace” the parabola the darker it becomes.)
Figure 5
To download a GSP animation of figure 5, go here and select “Animate Point.”
5. Geometer’s Sketchpad allows for two alternate constructions of parabolas as well.
a. The parabola in figure 6 has been created by tracing the perpendicular line FE as point C is dragged along segment BD.
Figure 6
b. The parabolas in figures 7 and 8 have been constructed using the locus command in the Construct Menu. (Figure 7 uses points C and F and figure 8 uses point C and line FE.) Note that this command yields the same results found above.
Figure 7
Figure 8
Connections to the other Conic Sections
6. What if the directrix was a circle instead of a line?
a. Consider figure 9 when point A is outside circle O and the line perpendicular to segment AB has been selected to trace. When point B is moved around the circle, a hyperbola is created.
Figure 9
b. Now consider figure 10 when point A is inside the circle. When point B is moved around the circle, an ellipse is created.
Figure 10
-
Author:
samsonwvis
-
Rate an answer:
14
follow this attachment
-
Author:
arynuigh
-
Rate an answer:
7
If you know the answer add it here!
Other related questions that may help you
-
Author:
milaguerra
-
Author:
jasperfzom
-
Rate an answer:
20
first you want to write the school name in the middle then write notice in the next line it is will be also in the middle then that the date then what is that body of the letter name class and destination that is how to write a notice
-
Author:
halfling2qat
-
Rate an answer:
9
-
Author:
maddie
-
Author:
anikahida
-
Rate an answer:
7
-
Author:
nico
-
Author:
crackersbrewer
-
Rate an answer:
8
Saurology is the study of ___________.
(A) Mosquitoes
(B) Snake
(C) Lizards
(D) Cockroach
answer...c) Lizard
-
Author:
nikkivewy
-
Rate an answer:
16
-
Author:
indy
-
Author:
katiexxgz
-
Rate an answer:
9
-
Author:
esperanzabranch
-
Rate an answer:
2