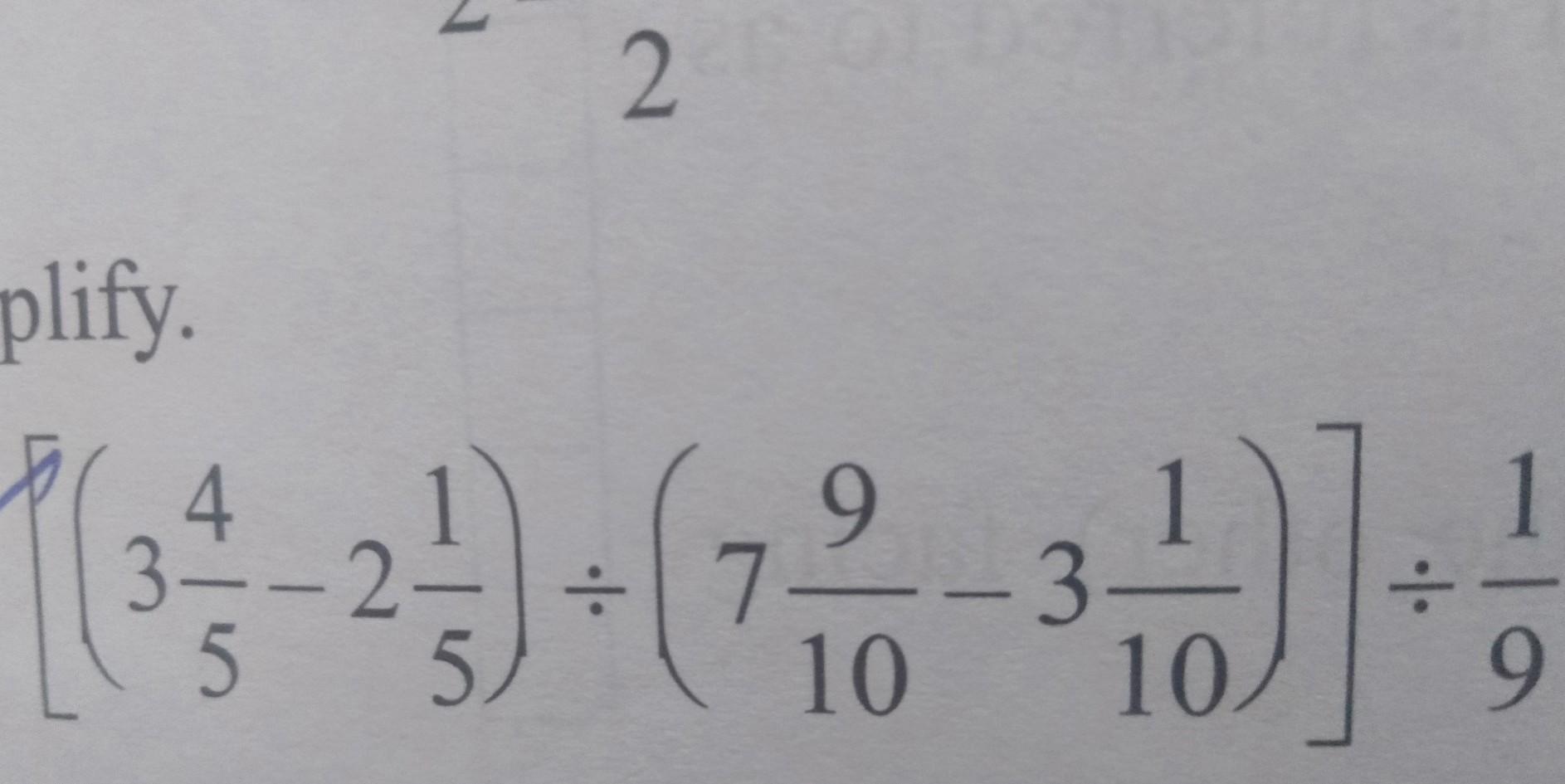what is the fractional part of answer based on the question
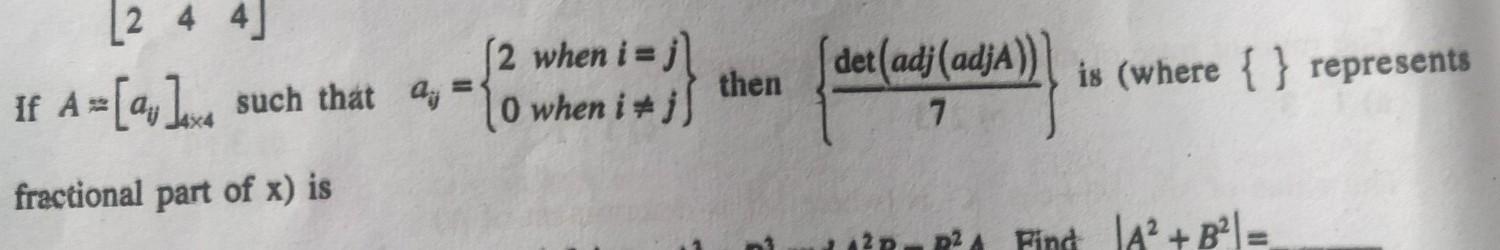
-
Subject:
Math -
Author:
chestergarza -
Created:
1 year ago
Answers 1
Answer:
[tex]\qquad\qquad\boxed{ \sf{ \: \bf \: \: \left \{ \: \dfrac{ det(adj(adjA))}{7} \right \} = \dfrac{1}{7} \: }} \\ \\ [/tex]
Step-by-step explanation:
Given that,
[tex]\sf \:A = [ a_{ij}]_{4 \times 4} \: such \: that \\ \\ [/tex]
[tex]\begin{gathered}\begin{gathered}\bf\: a_{ij} = \begin{cases} &\sf{2, \: \: when \: i = j} \\ &\sf{0, \: \: when \: i \: \ne \: j} \end{cases}\end{gathered}\end{gathered} \\ \\ [/tex]
So, it means
[tex]\sf\implies \sf \: A=\left[\begin{array}{cccc}2&0&0&0\\0&2&0&0\\0&0&2&0\\0&0&0&2\end{array}\right] \\ \\ [/tex]
So,
[tex]\bf\implies \: |A| = 2 \times 2 \times 2 \times 2 = 16 \\ \\ [/tex]
Now, Consider
[tex]\sf \: |adj(adjA)| \\ \\ [/tex]
[tex]\sf \: = \: { |A| }^{(4 - 1)^{2} } \\ \\ [/tex]
[tex]\boxed{ \sf{ \: \because \: |adj(adjA)| = { |A| }^{ {(n - 1)}^{2} } \: }} \\ \\ [/tex]
[tex]\sf \: = \: { |A| }^{ {(3)}^{2} } \\ \\ [/tex]
[tex]\sf \: = \: {16}^{9} \\ \\ [/tex]
[tex]\sf \: = \: {( {2}^{4} )}^{9} \\ \\ [/tex]
[tex]\sf \: = \: {2}^{36} \\ \\ [/tex]
Now, Consider
[tex]\sf \: \: \left \{ \: \dfrac{ det(adj(adjA))}{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ |adj(adjA)| }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ {2}^{36} }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ {2}^{3 \times 12} }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ {( {2}^{3}) }^{12} }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ {( 8) }^{12} }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{ {(7 + 1) }^{12} }{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{C_0 + C_1(7) + C_2( {7}^{2} ) + ... + C_{12}( {7}^{12})}{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{1 +7[ C_1+ C_2( {7}^{} ) + ... + C_{12}( {7}^{11})]}{7} \right \} \\ \\ [/tex]
[tex]\sf \: \: = \: \left \{ \: \dfrac{1 }{7} +C_1+ C_2( {7}^{} ) + ... + C_{12}( {7}^{11})\right \} \\ \\ [/tex]
[tex]\sf \: = \: \dfrac{1}{7} \\ \\ [/tex]
Hence,
[tex]\sf\implies \bf \: \: \left \{ \: \dfrac{ det(adj(adjA))}{7} \right \} = \dfrac{1}{7} \\ \\ [/tex]
[tex]\rule{190pt}{2pt}[/tex]
Additional Information
If A and B are square matrices of order n, then
[tex]\sf \: |AB| = |A| \: |B| \\ \\ [/tex]
[tex]\sf \: |adjA| = { |A| }^{n - 1} \\ \\ [/tex]
[tex]\sf \: |A \: adjA| = { |A| }^{n} \\ \\ [/tex]
[tex]\sf \: | {A}^{ - 1} | = { |A| }^{ - 1} \\ \\ [/tex]
[tex]\sf \: |A| = |A'| \\ \\ [/tex]
[tex]\sf \: |adj(adj \: A)| = { |A| }^{ {(n - 1)}^{2} } \\ \\ [/tex]
-
Author:
angelosqdq
-
Rate an answer:
7