Two perpendicular sides of night angled triangle are 12 cm and 35 cm. Find hypotonius.
Answers 2
This theorem states that, In a right angled triangle, the square of the hypotenuse is equal to the sum of square of the other two sides.
Normally, to solve for right angled triangles, we use Pythagoras theorem.
As we went through the concept about Pythagoras theorem, Now Let's, move on finding the solution for our question.
We have been given that, Two perpendicular sides of a right angled triangle are 12 cm and 35 cm respectively. And We have been asked to find the hypotenuse.
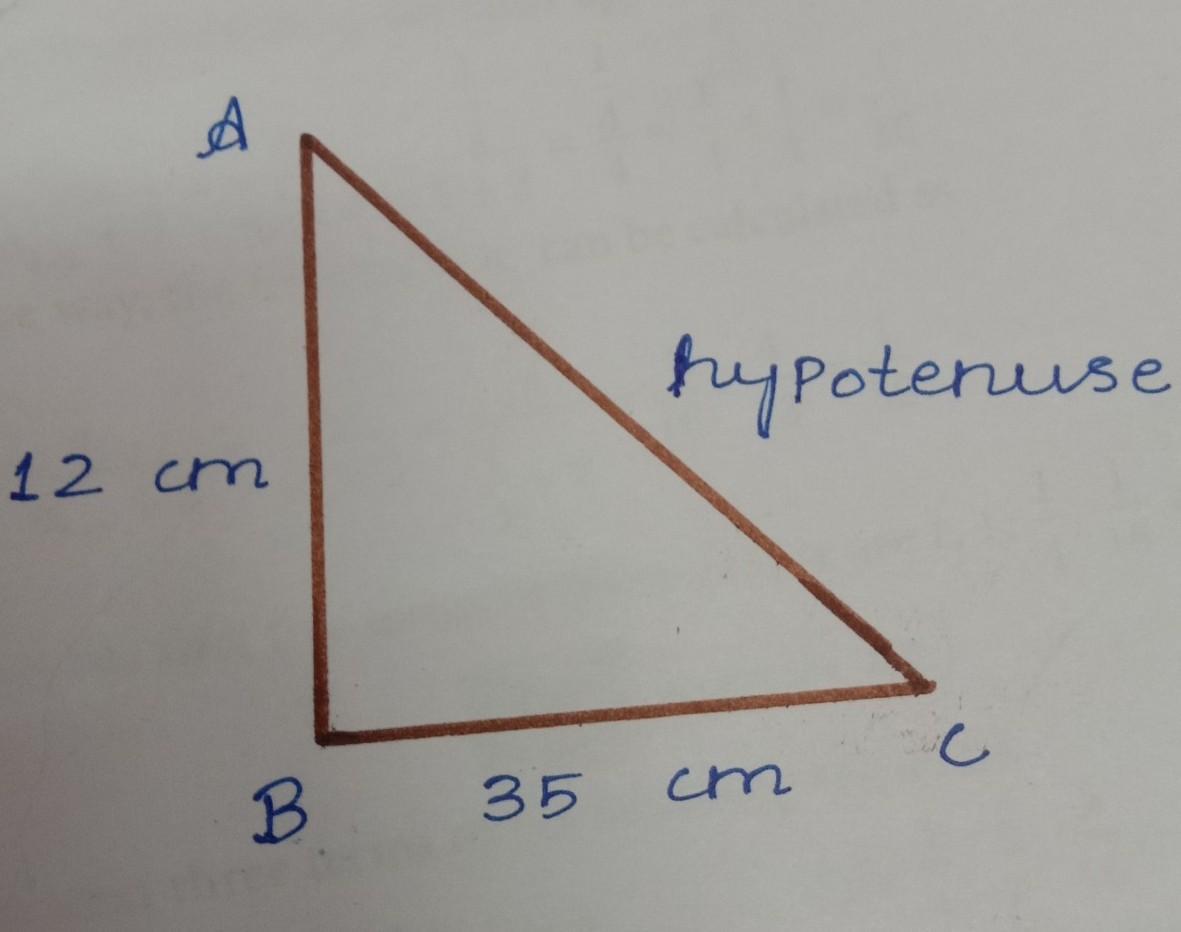
(Refer the attachment for the figure)
Given,
- AB = 12 cm
- BC = 35 cm
We know that,
[tex]{\boxed{\bullet\:{AB^2\:+\:BC^2\:=\:AC^2}}}[/tex]
Substituting values in Formula, we get,
[tex]\sf\implies{AB^2\:+\:BC^2\:=\:AC^2}[/tex]
[tex]\sf\implies{(12)^2\:+\:(35)^2\:=\:AC^2}[/tex]
[tex]\sf\implies{144\:+\:1225\:=\:AC^2}[/tex]
[tex]\sf\implies{1369\:=\:AC^2}[/tex]
[tex]\sf\implies{AC\:=\:{\sqrt{1369}}}[/tex]
[tex]\sf\implies{AC\:=\:37\:cm}[/tex]
Hence, the hypotenuse in the right angled triangle ABC is 37 cm.
-
Author:
erikacxgi
-
Rate an answer:
9
Answer:
The hypotenuse is 37 cm
Step-by-step explanation:
To solve this question we will be needing the pythagoras theorem which is [tex]h^{2}=p^{2}+b^{2}[/tex] where h is hypotenuse p is perpendicular and b is base
Now we are given 2 perpendicular lines which means both of them are perpendicular and base by putting it in the formula we will get
[tex]h^{2} = 12^{2} +35^{2} \\h^{2} =144+1225\\h^{2} = 1369\\h=\sqrt{1369} \\h= 37[/tex]
-
Author:
mittenswu
-
Rate an answer:
3
