Solve this Linear Equation::Answer Should be ----- [tex] - 1[/tex]Please No Rubbish, Answer it correctly, Answer Matching along with correct Process will get Brainlist.......
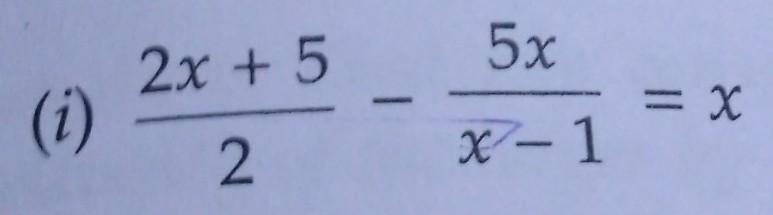
Answers 2
Answer:
[tex]\qquad\qquad\qquad\boxed{ \sf{ \: \bf \:x = - 1 \: }} \\ \\ [/tex]
Step-by-step explanation:
Given equation is
[tex]\sf \:\dfrac{2x + 5}{2} - \dfrac{5x}{x - 1} = x \\ \\ [/tex]
[tex]\sf \:\dfrac{(2x + 5)(x - 1) - 2(5x)}{2(x - 1)} = x \\ \\ [/tex]
[tex]\sf \:\dfrac{ {2x}^{2} + 5x - 2x - 5 - 10x}{2x - 2} = x \\ \\ [/tex]
[tex]\sf \:\dfrac{ {2x}^{2} + 3x - 5 - 10x}{2x - 2} = x \\ \\ [/tex]
[tex]\sf \:\dfrac{ {2x}^{2} - 7x - 5}{2x - 2} = x \\ \\ [/tex]
[tex]\sf \: {2x}^{2} - 7x - 5 = x(2x - 2) \\ \\ [/tex]
[tex]\sf \: {2x}^{2} - 7x - 5 = {2x}^{2} - 2x \\ \\ [/tex]
[tex]\sf \: - 7x - 5 = - 2x \\ \\ [/tex]
[tex]\sf \: - 7x + 2x = 5 \\ \\ [/tex]
[tex]\sf \: - 5x = 5 \\ \\ [/tex]
[tex]\sf \:x = \dfrac{5}{ - 5} \\ \\ [/tex]
[tex]\sf\implies \bf \:x = - 1 \\ \\ [/tex]
Verification
[tex]\sf \:\dfrac{2x + 5}{2} - \dfrac{5x}{x - 1} = x \\ \\ [/tex]
On substituting x = - 1, we get
[tex]\sf \:\dfrac{2( - 1) + 5}{2} - \dfrac{5( - 1)}{ - 1 - 1} = - 1 \\ \\ [/tex]
[tex]\sf \:\dfrac{ - 2 + 5}{2} - \dfrac{ - 5}{ - 2} = - 1 \\ \\ [/tex]
[tex]\sf \:\dfrac{3}{2} - \dfrac{5}{2} = - 1 \\ \\ [/tex]
[tex]\sf \:\dfrac{3 - 5}{2} = - 1 \\ \\ [/tex]
[tex]\sf \:\dfrac{ - 2}{2} = - 1 \\ \\ [/tex]
[tex]\sf \: - 1 = - 1 \\ \\ [/tex]
Hence, Verified
-
Author:
amber
-
Rate an answer:
12
Answer:
mark me brainliest pls and follow me on brainly
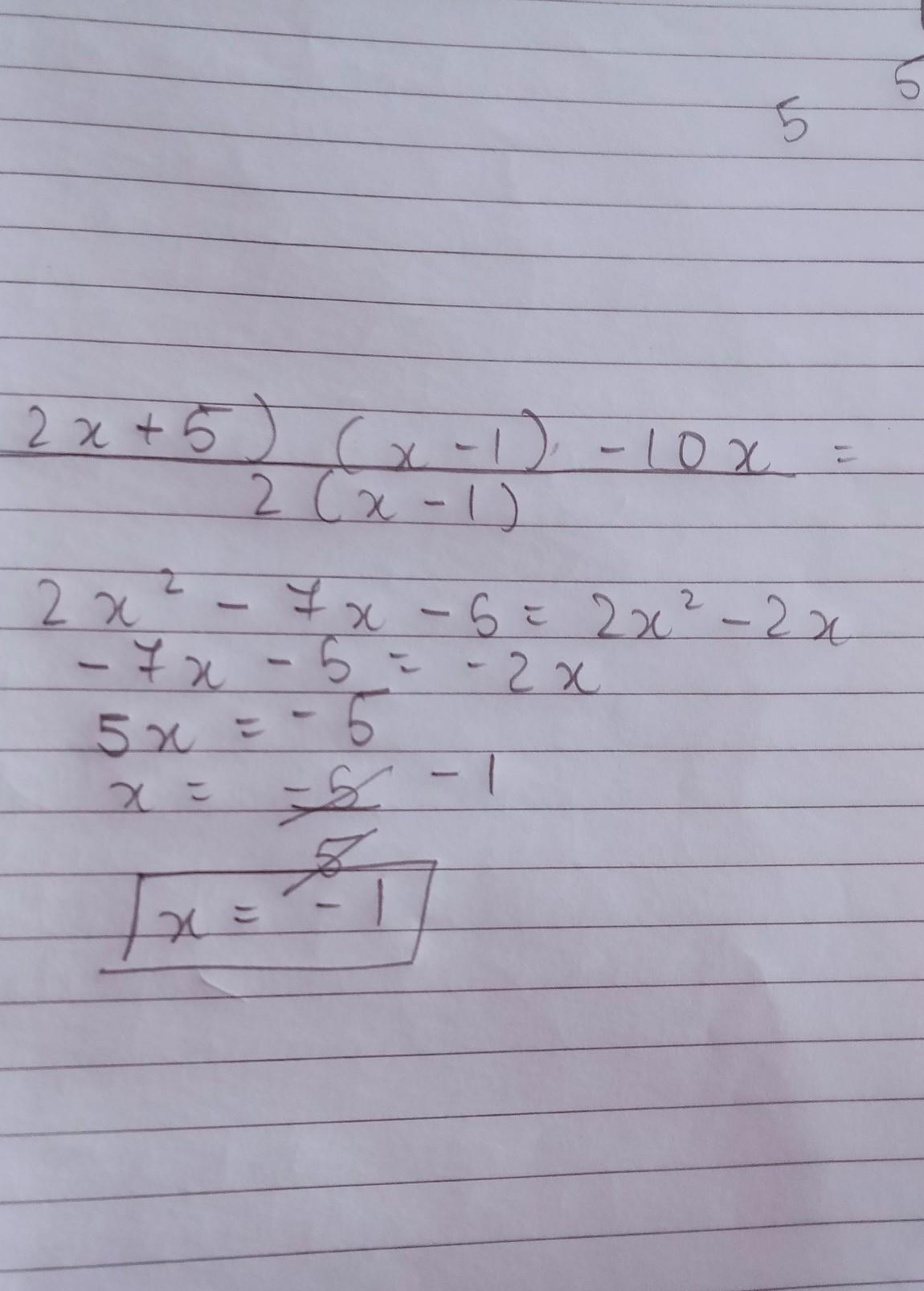
-
Author:
nathan
-
Rate an answer:
0
