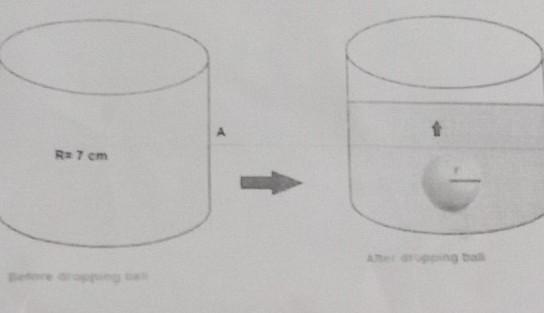
Dev was doing an experiment to find the radius r of a sphere. For this he took a cylindrical container with radius R = 7 cm and height = 10cm. He filled the container almost half by water as shown in the left figure. Now he dropped the yellow sphere in the container. Now he observed as shown in the right figure the water level in the container raised from A to B equal to 3.40 cm.i) What is the approximate radius of the sphere ?ii) What is the volume of the cylinder ?iii) What is the volume of the sphere ?iv) How many litres water can be filled in the full container ?v) What is the surface area of the sphere ?​

Answer:

The probability of getting not blue marbles will be 13/30

Answer:

Let box contains red marbles be R1, R2, R3, R4, R5, R6, R7, R8, R9, R10

Let box contains with white marbles be W1, W2, W3

Let box contains with blue marbles be B1, B2, B3, B4, B5, B6, B7, B8, B9, B10, B11, B12, B13, B14, B15, B16, B17

Let S be the sample space

n(S) =R1, R2, R3, R4, R5, R6, R7, R8, R9, R10, W1, W2, W3, B1, B2, B3, B4, B5, B6, B7, B8, B9, B10, B11, B12, B13, B14, B15, B16, B17

n(S) =30

Let A be the event that marble picked from box is not blue

P(A) =R1, R2, R3, R4, R5, R6, R7, R8, R9, R10, W1, W2, W3

P(A) =13

By definition of probability,

P(A) =n(A) /n(S)

13/30

Ans :- P(A) =13/30

Explanation:

answer 1. curved surface separating two media air and glass formula

=Na and Ng

answer 2.radius of curvature approaches to infinity formula

=R/1k

where R is the radius and K is centre of the curvature

hope it helps you

mark as a brainliest ✨

let us consider the height of the tower 'h'

we know that 'h'= AC tan 30 degree = BC tan 30 degree

We know that AC=BC [∵ radius of circle]

Hence, we can say that △ABC is an isosceles triangle with AC=BC.

So, ∠ABC=∠BAC ...(2)

But ∠ACB=60

∘

[given]

⇒∠ABC+∠BAC+∠ACB=180

∘

⇒∠ABC+∠ABC+60

∘

=180

∘

[from (2)]

⇒2×∠ABC=120

∘

∴∠ABC=∠BAC=60

∘

Hence △ABC is an equilateral triangle.

∴AB=BC=CA=a ...(3)

∴h=atan30

∘

[form equation (1)]

=

3

a

Step-by-step explanation:

Solution

verified

Verified by Toppr

Correct option is C)

Let us consider the height of the tower as h

We know that, h=ACtan30

∘

=BCtan30

∘

...(1)

We know that AC=BC [∵ radius of circle]

Hence, we can say that △ABC is an isosceles triangle with AC=BC.

So, ∠ABC=∠BAC ...(2)

But ∠ACB=60

∘

[given]

⇒∠ABC+∠BAC+∠ACB=180

∘

⇒∠ABC+∠ABC+60

∘

=180

∘

[from (2)]

⇒2×∠ABC=120

∘

∴∠ABC=∠BAC=60

∘

Hence △ABC is an equilateral triangle.

∴AB=BC=CA=a ...(3)

∴h=atan30

∘

[form equation (1)]

=

3

a

Sunita Lyn Williams (née Pandya; born September 19, 1965) is an Indian - American astronaut and United States Navy officer who formerly held the records for most spacewalks by a woman (seven) and most spacewalk time for a woman (50 hours, 40 minutes)...

sorry I don't know urdu....