Find the slant height of a cone whose, (i) Base radius - 14 cm, height -0.48 m (ii) Base diameter = 70 cm, curved surface area 4070 cm
Answers 2
Answer:
(i) 50cm
(ii) 37 cm
Step-by-step explanation:
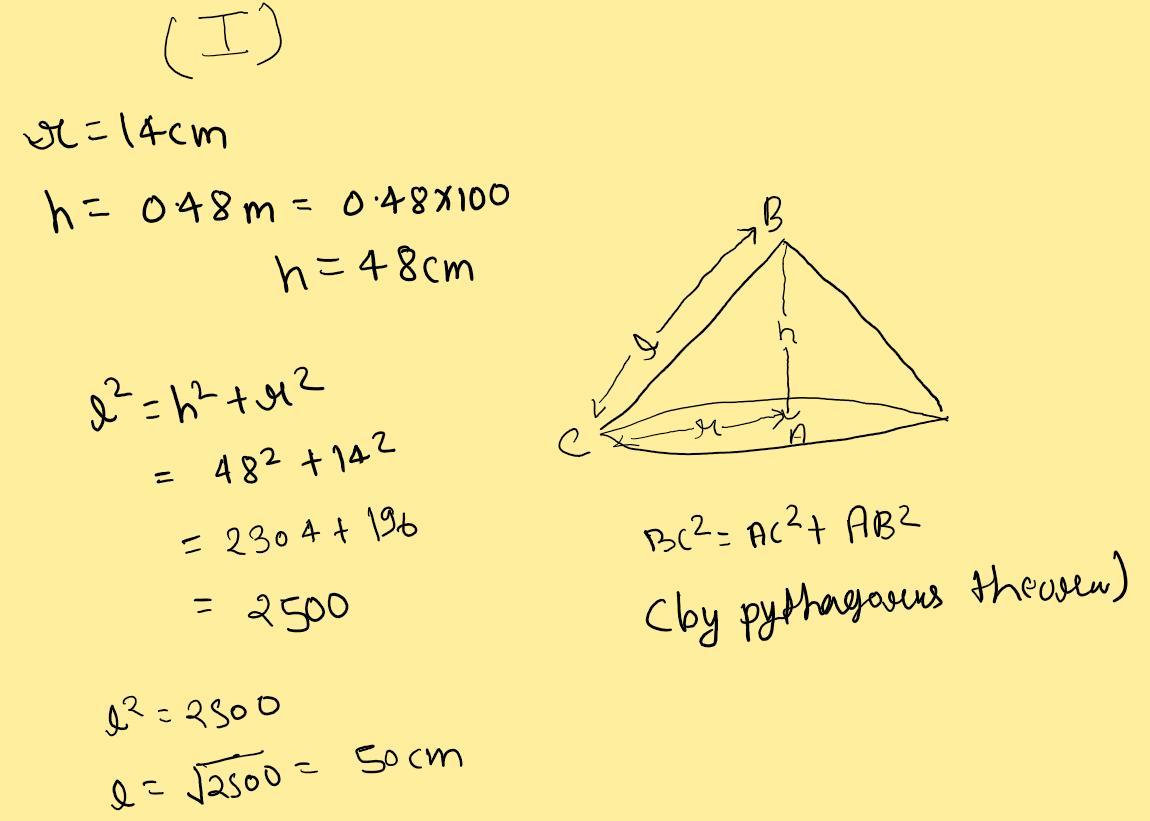
Part (i) : -
Given that
Radius of cone(r) = 14cm
Height of the cone(h) = 0.48m
= (0.48 × 100)cm
h = 48 cm
Slant height of the cone (l) ?
We know that
l² = h² + r²
l² = 48² + 14²
l² = 2304 + 196
l² = 2500
l = √2500
l = 50 cm
Thus slant height of the cone is 50 cm
Part (ii) : -
Given that
Base diameter of cone = 70cm
Radius of cone(r) = 70/2
r = 35 cm
and
Curved surface area of the cone = 4070 cm
πrl = 4070
π × 35 × l = 4070
(22/7) × 35 × l = 4070
22 × 5 × l = 4070
110 × l = 4070
l = 4070/110
l = 407/11
l = 37
l = 37 cm
Thus slant height of the cone is 37 cm
Note:-
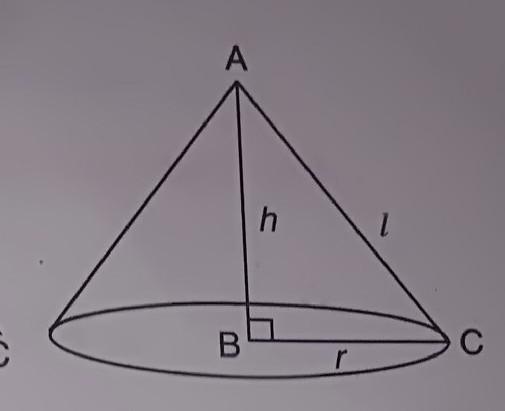
CSA of Cone = πrl
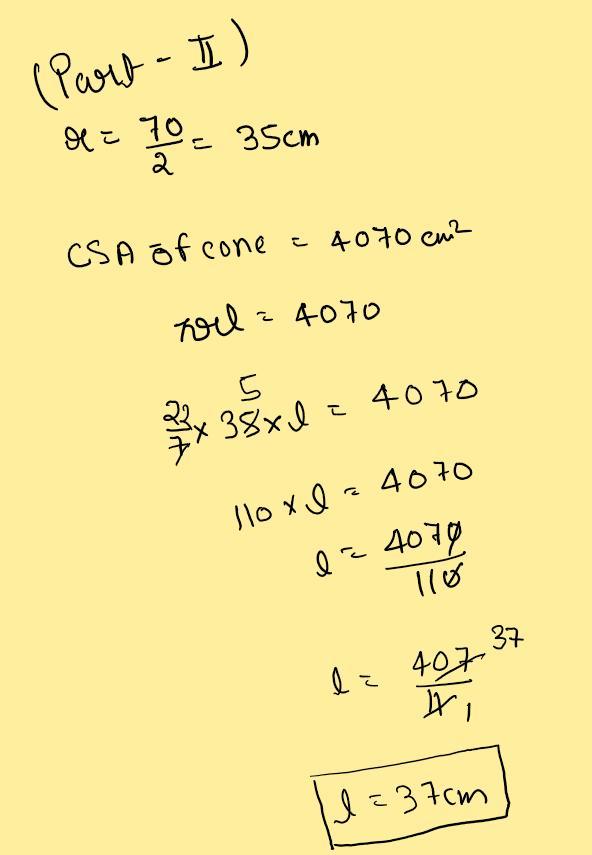
-
Author:
corkyrpvz
-
Rate an answer:
1
- Base radius is 14 cm of a cone
- Height is 0.48 m of that cone
- Slant height (l) of the cone ?
Using formula of calculating the slant height of cone (l),
- l² = h² + r²
Here,
- l is slant height
- h is height
- r is radius
But before putting the values in it we would be changing the unit of height (h) which is in metres into centimetres.
➺ h = 0.48 × 100
➺ h = (48/100) × 100
➺ h = 48 cm
Therefore, height of cone in centimetres is 48cm.
Putting all the required values,
➺ l² = (48)² + (14)²
➺ l² = (48 × 48) + (14 × 14)
➺ l² = (2304) + (196)
➺ l² = 2304 + 196
➺ l² = 2500
➺ l = √2500
➺ l = 50
Therefore, slant height (l) of the cone is 50 cm.
_____________________________________
Solution 2 :-Information provided with us :- Curved surface area (C.S.A) of the cone is 4070 cm.
- Diameter is of 70 cm.
- Slant height (l) of the cone.
★ Curved surface area of cone :-
- C.S.A. = πrl
Here,
- Value of π is 22/7
- r is radius
- l is slant height
First of all we would be finding out the radius of the cone as we have been provided with its diameter.
As we know that,
➺ r = d / 2
By using it we gets,
➺ r = 70 / 2
➺ r = 35
Therefore, radius of the cone is of 35 cm.
Putting all the values in the formula,
➺ 4070 = (22/7) (35) (l)
➺ 4070 = 22/7 × 35 × l
➺ 4070 = 22 × 35 × l / 7
➺ 4070 = 22 × 5 × l
➺ l = 4070 / 22 × 5
➺ l = 814 / 22
➺ l = 407 / 11
➺ l = 37
Therefore, slant height (l) of the cone is of 37cm.
Additional Information :★ Volume of cone:-
- V = ⅓ πr²h
★ Total Surface Area of cone:-
- T.S.A. = πrl + πr²
Some more formulas related to concept surface area and volume :
★ Curved surface area of cylinder:-
- C.S.A. = 2πrh
★ Total surface area of cylinder:-
- T.S.A. = 2πr (h + r)
★ Volume of cylinder:-
- V = πr²h
★ Area of cross-section:-
- Area of cross-section = πr²
★ Volume of sphere:-
- V = 4/3 × πr³
★ Volume of cube:-
- V = a³
In these formulas,
- r is radius
- h is height
- a is side of cube
-
Author:
gordon9bwt
-
Rate an answer:
8
