an arch is in the form of a semi ellipse. it is 50 metres wide at the base and has a height of 20 metres. how wide is the arch at the heigh of 10 metres above the base?
Answers 1
[tex]\large\underline{\sf{Solution-}}[/tex]
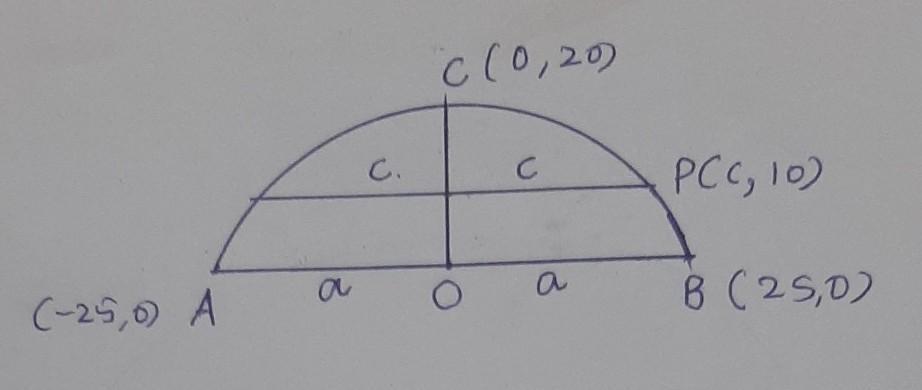
Given that, an arch is in the form of a semi ellipse, which is 50 metres wide at the base and has a height of 20 metres.
Let assume that the equation of ellipse be
[tex]\rm \: \dfrac{ {x}^{2} }{ {a}^{2} } + \dfrac{ {y}^{2} }{ {b}^{2} } = 1 \\ [/tex]
As it is given that, it is 50 m wide from the base and 20 m high from base.
[tex]\rm\implies \:2a = 50 \: \: \: and \: \: \: b = 20 \\ [/tex]
[tex]\rm\implies \:a = 25 \: \: \: and \: \: \: b = 20 \\ [/tex]
So, equation of ellipse can be rewritten as
[tex]\rm \: \dfrac{ {x}^{2} }{ {25}^{2} } + \dfrac{ {y}^{2} }{ {20}^{2} } = 1 \\ [/tex]
[tex]\rm \: \dfrac{ {x}^{2} }{625} + \dfrac{ {y}^{2} }{400} = 1 - - - (1) \\ [/tex]
Let assume that semi - ellipse is 2c metres wide at the height of 10 m from the base. So, it means (c, 10) lies on equation (1).
So,
[tex]\rm \: \dfrac{ {(c)}^{2} }{625} + \dfrac{ {10}^{2} }{400} = 1 \\ [/tex]
[tex]\rm \: \dfrac{ {c}^{2} }{625} + \dfrac{100}{400} = 1 \\ [/tex]
[tex]\rm \: \dfrac{ {c}^{2} }{625} + \dfrac{1}{4} = 1 \\ [/tex]
[tex]\rm \: \dfrac{ {c}^{2} }{625} = 1 - \dfrac{1}{4} \\ [/tex]
[tex]\rm \: \dfrac{ {c}^{2} }{625} = \dfrac{4 - 1}{4} \\ [/tex]
[tex]\rm \: \dfrac{ {c}^{2} }{625} = \dfrac{3}{4} \\ [/tex]
[tex]\rm \: {c}^{2} = \dfrac{3 \times 625}{4} \\ [/tex]
[tex]\rm\implies \:c \: = \: \dfrac{25 \sqrt{3} }{2} \: m \\ [/tex]
Hence,
[tex]\rm\implies \:Width = 2c \: = \: 25 \sqrt{3} \: m \\ [/tex]
[tex]\rule{190pt}{2pt}[/tex]
Additional Information :-
[tex]\begin{gathered}\boxed{\begin{array}{c|c} \bf & \bf \dfrac{ {x}^{2} }{ {a}^{2} } + \dfrac{ {y}^{2} }{ {b}^{2} } = 1 , \: (a > b)\\ \frac{\qquad \qquad}{} & \frac{\qquad \qquad}{} \\ \sf Vertex & \sf ( \pm \: a, \: 0) \\ \\ \sf Focus & \sf ( \pm \: ae, \: 0)\\ \\ \sf eccentricity & \sf e = \sqrt{1 - \dfrac{ {b}^{2} }{ {a}^{2} } } \\ \\ \sf Length \: of \: major \: axis & \sf 2a\\ \\ \sf Length \: of \: minor \: axis & \sf 2b\\ \\ \sf Length \: of \: latus \: rectum & \sf \dfrac{ {2b}^{2} }{a} \\ \\ \sf Distance \: between \: focus & \sf 2ae \end{array}} \\ \end{gathered} \\ [/tex]
-
Author:
mikey2vms
-
Rate an answer:
5
