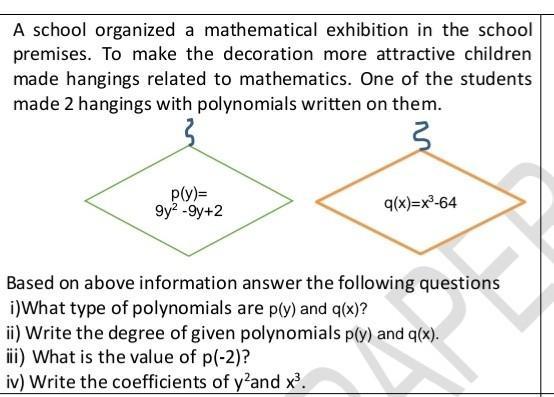
A school organized a mathematical exhibition in the school premises. To make the decoration more attractive children made hangings related to mathematics. One of the students made 2 hangings with polynomials written on them

Answers 2

Answer:

i) p(y) is quadratic polynomial and q(x) is a cubic polynomial

ii) degree of p(y)=2 , degree of q(x)=3

iii)p(-2)= 9(-2)²-9(-2)+2

= 9(4)+18+2

=36+18+2

=56

iv) coeff of y²= 9

coeff of x³= 1

The answers are:

i) p(y) is a trinomial and q(x) is a binomial.

ii) The degree of p(y) is 2, and the degree of q(x) is 3.

iii) The value of p(-2) = 56.

iv) The coefficient [tex]y^2[/tex] is 9, and the coefficient [tex]x^3[/tex] is 1.

Step-by-step explanation:

Given: Two polynomials [tex]p(y) = 9y^2 -9y+ 2[/tex] and [tex]q(x) = x^3 -64[/tex]

Solutions:

i) p(y) has three terms, hence, p(y) is a trinomial.

q(x) has two terms, hence, q(x) is a binomial.

ii) A polynomial's degree is the highest or the greatest power of a variable in a polynomial equation.

Thus, the degree of p(y) is 2, and the degree of q(x) is 3.

iii)The value of p(-2) can be calculated by putting [tex]y = -2[/tex] in the equation:

[tex]p(-2)= 9(-2)^2-9(-2)+2[/tex]

[tex]= 9(4)+18+2[/tex]

[tex]=36+18+2[/tex]

[tex]=56[/tex]

Thus, p(-2) = 56

iv) The coefficients are the numbers written before the variables.

Thus, the coefficient [tex]y^2[/tex] is 9, and the coefficient [tex]x^3[/tex] is 1.