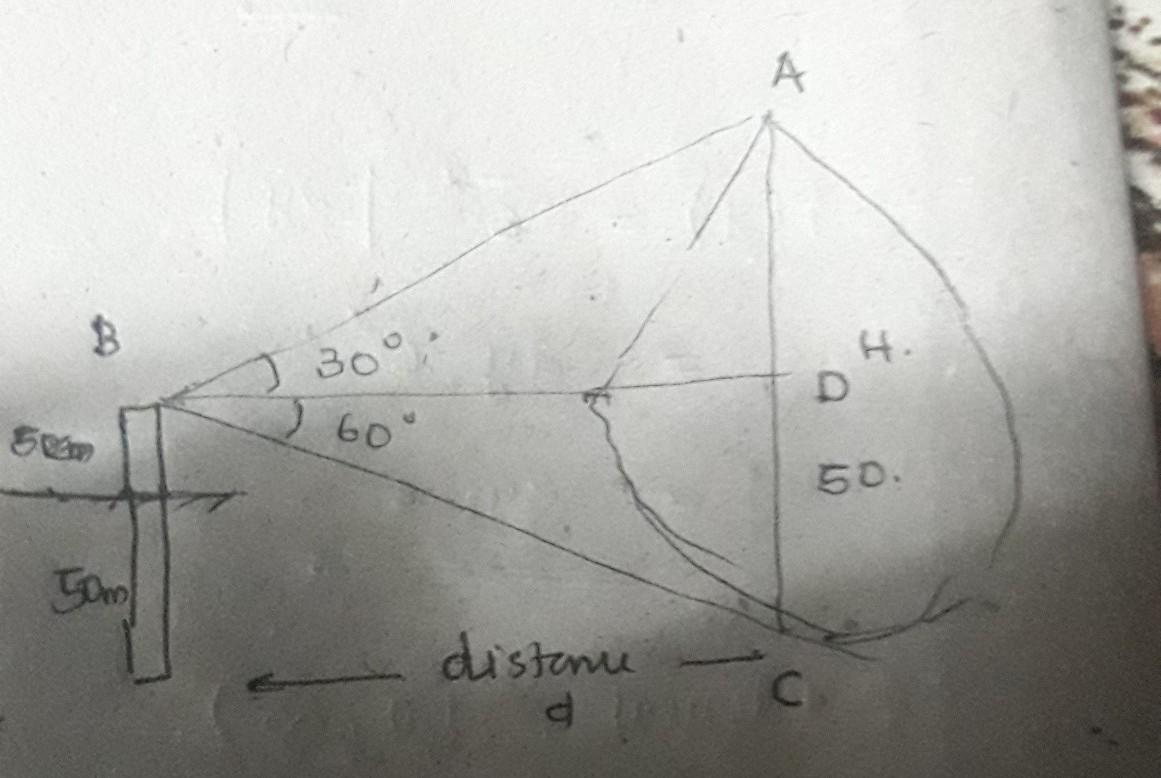
A girl on a ship standing on a wooden platform, which is 50 m above water level, observes the angle of elevation of the top of a hill as 30° and the angle of depression of the base of the hill as 60°. Calculate the distance of the hill from the platform and the height of the hill.​

Answers 2

Step-by-step explanation:

just draw diagram properly and then answer will come correct

answer img

Given

  • height of the wooden platform equal to 50 m
  • angle of elevation 30°
  • angle of depression is 60 degree

To find

  • the height of the hill
  • the distance between the hill and the point where the girls stands.

Solution

from the figure we can write, considering the triangle ABD

tan30 = AD/BD

or, tan30 = AD/d

or, d = AD/tan30

or, d= √3AD ....(1)

considering the triangle BDC

tan60 = DC/BD

or, tan60 = 50/d

or, d= 50/√3

or, d = 28.86m

distance of the girl from the hill is 28.86m

using equation 1

AD = 28.8/√3

Or, AD = 16.6m

therefore the height of the hill, AD + 50

Or, 16.6 + 50 = 66.6 m

answer img

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

What was the theme of last year's Cyber Security?​

Answer:

The theme for this year is 'Do Your Part' #BeCyberSmart. As digital services are on the rise, so are cyberattacks. Cyber Security has become more important than ever in today's digital life.

Answer:

Do Your Part. #BeCyberSmart.”

Explanation:

hope this helps

81. Which one of the following statements is true about fossil fuels ? 1) They are renewable resources. 2) They are found within the top layers of the Earth's crust. 3) They are formed over the course of ten years. 4) They are the remains of organisms. ​

Explanation:

Which one of the following statements is true about fossil fuels ?

1) They are renewable resources.

2) They are found within the top layers of the Earth's crust.

3) They are formed over the course of ten years.

4) They are the remains of organisms.

correct option is 3)

Answer:

Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams.

Explanation:

Fossil fuels can be made in the laboratory. (F)

Petrochemicals indeed are made in laboratories by the process of oil refining, but Coal, Petroleum and Natural gas, cannot be prepared in laboratories as they're the product of extraction of fossils which are buried millions of years ago. That means it takes many years for coal and petrol to form and convert into fossil fuels.

Formula of Copper zincate?​

Explanation:

C⁸H¹⁶CuN⁸Zn

pubchem CID-171918

Answer:

sister will we become siblings

because your thoughts and thinking is legendry

we achieve highest goals in our life

In the expansion of the function e sinx , the coefficient of x is (a)-2 (b) 2 (c) 3/2 (d) None of these​

Answer:

option b) 2 is the answer

Step-by-step explanation:

[tex]\huge\colorbox{orange}{please{mark}{\colorbox{orange} {me as brainlist}}}[/tex]

Other Math Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years