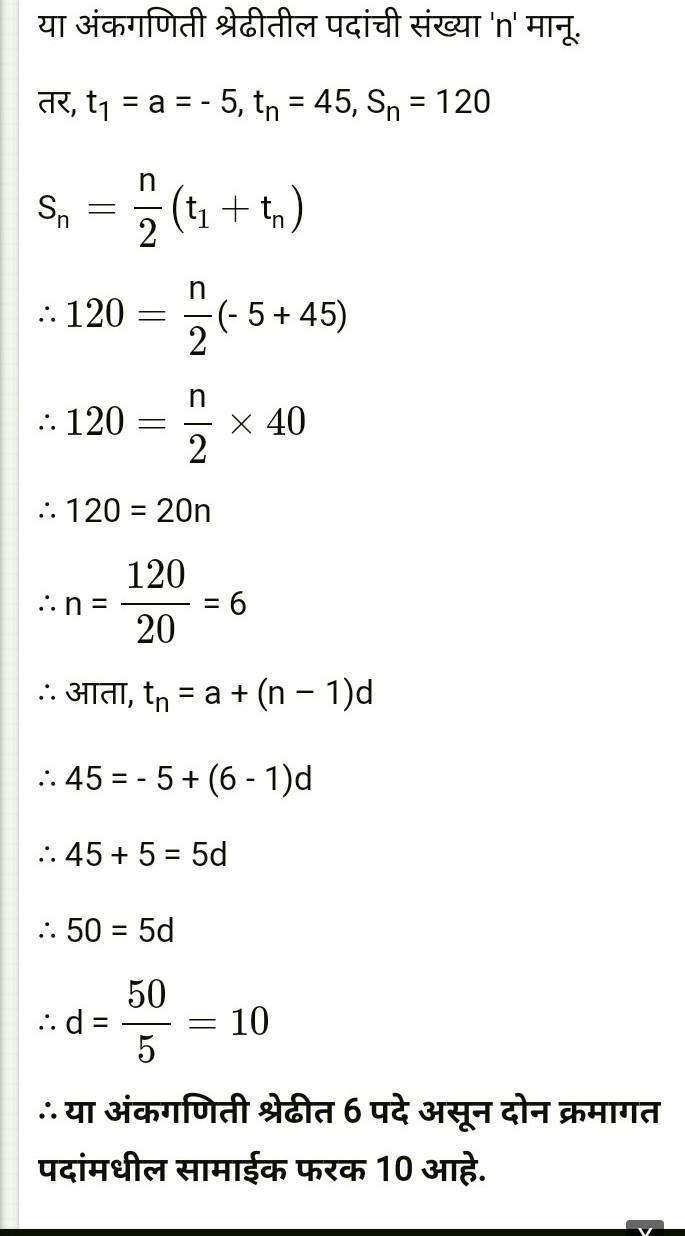If the area of two similar triangles are 121 square cm and 289 square cm respectively. Then find the ratio between its corresponding sides.

The ratio of corresponding sides of the triangles is [tex]17:11[/tex] .

Given,

Area of two similar triangles as,

[tex]A_{1}=121cm^{2}[/tex]

[tex]A_{2}=289cm^{2}[/tex]

To find,

The ratio between the corresponding sides of the given triangles.

Solution,

We know that,

Two similar triangles have corresponding sides in equal proportion.

And also,

The ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.

⇒[tex]\frac{A_{2}}{A_{1}}=(\frac{Side_{2}}{Side_{1}})^{2}[/tex]

So,

The ratio of the sides of the triangles will be,

[tex]\frac{x^{2}}{y^{2}} = \frac{A_{2}}{A_{1}}[/tex]

⇒[tex]\frac{x^{2}}{y^{2}} =\frac{289}{121}[/tex]

⇒[tex]\frac{x}{y} =\sqrt{\frac{289}{121} }[/tex]

⇒[tex]\frac{x}{y} =\frac{17}{11}[/tex]

Therefore, the ratio of the corresponding sides of the triangles is [tex]17:11[/tex]

The ratio between its corresponding sides is 11 : 17.

------------------------------------------------------------------------------------------

To find Area(triangle STU) we must use the Theorem of Areas of Similar Triangles.

What are similar triangles?

Two triangles are said to be similar if their corresponding angles are equal and their corresponding sides are proportional to each other.

What is the Theorem of Areas of Similar Triangles?

The theorem states that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

For example: if ΔABC and ΔPQR are two similar triangles then we can say that,

[tex]\boxed{\bold{\frac{Area (\triangle ABC)}{Area(\triangle PQR)} = \bigg(\frac{AB}{PQ}\bigg)^2 = \bigg(\frac{BC}{QR}\bigg)^2= \bigg(\frac{AC}{PR}\bigg)^2 }}[/tex]

---------------------------------------------------------------------------------------------

Let's say the two similar triangles be Δ ABC and Δ PQR and we will find the ratio of its corresponding sides AB and PQ respectively.

So, here we have

Area (Δ ABC) = 121 cm²

Area (Δ PQR) = 289 cm²

By using the above theorem of the areas of similar triangles, we get

[tex]\frac{Area (\triangle ABC)}{Area(\triangle PQR)} = \bigg(\frac{AB}{PQ}\bigg)^2[/tex]

• on substituting the given values

[tex]\implies \frac{121}{289} = \bigg(\frac{AB}{PQ}\bigg)^2[/tex]

• taking square root on both sides

[tex]\implies \sqrt{\frac{121}{289} } = \sqrt{ \bigg(\frac{AB}{PQ}\bigg)^2}[/tex]

• 11² = 121 and 17² = 289

[tex]\implies \sqrt{\frac{11^2}{17^2} } = \sqrt{ \bigg(\frac{AB}{PQ}\bigg)^2}[/tex]

[tex]\implies \frac{AB}{PQ} =\frac{11}{17}[/tex]

[tex]\implies \bold{AB : PQ = 11: 17}[/tex]

Thus, the ratio between its corresponding sides AB and PQ are 11 : 17.

----------------------------------------------------------------------------------------

brainly.in/question/180664

brainly.in/question/28614466