In the adjoining diagram AB is perpendicular to PX. If CXB is a straight line and AP = BP, prove that CB= CX+XA​

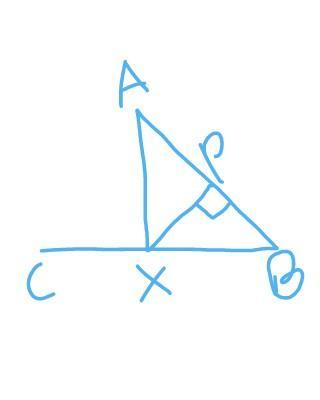
question img

Answers 1

Step-by-step explanation:

In △OAP and △OBQ,

AP=BQ(given)

∠OAP=∠OBQ=90

∘

∠OAP=∠OBQ(vertically opposite angles)

∴△OAP is congruent to △OBQ by AAS axiom

∴OA=OB by C.P.C.T.

and OP=OQ by C.P.C.T

⇒O is the midpoint of line segments AB and PQ

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

nounsto my mother, my ........ (safe) is of utmost importance ​

Answer:

safety.................

Answer:

my safety is of upmost importance

Explanation:

please mark my answer brilentest
What is the mass of earth?Hello Nancy​

Explanation:

An Earth mass, is a unit of mass equal to the mass of the planet Earth. The current best estimate for the mass of Earth is M⊕ = 5.9722×10²⁴ kg, with a standard uncertainty of 6×10²⁰ kg. The recommended value in 1976 was ×10²⁴ kg. It is equivalent to an average density of 5515 kg·m⁻³.

Unit of: mass

Answer:

5.972 × 10^24 kg

Explanation:

प्रश्न 8 किसने किससे कहा ? क "मैं नहीं जानती। अपने मन की बात वे राम की ही बताएँगे​

Answer:

“मैं नहीं जानती । अपने मन की बात वे राम को ही बताएँगे ।” कैकेयी ने महामंत्री से कहा।

Mark my answer as brainlist.

Factorisation of 108 is shown below. 108 = 2 x 2 x 3 x 3 x 3 Which of these would be a factor of 108? Select all the correct options A. 2 B. 3 C. 2 x 3 D. 2 x 2 x 3 E. 2 x 2 x 3 x 3 x 3

Answer:

The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, and 108.

Other Math Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years