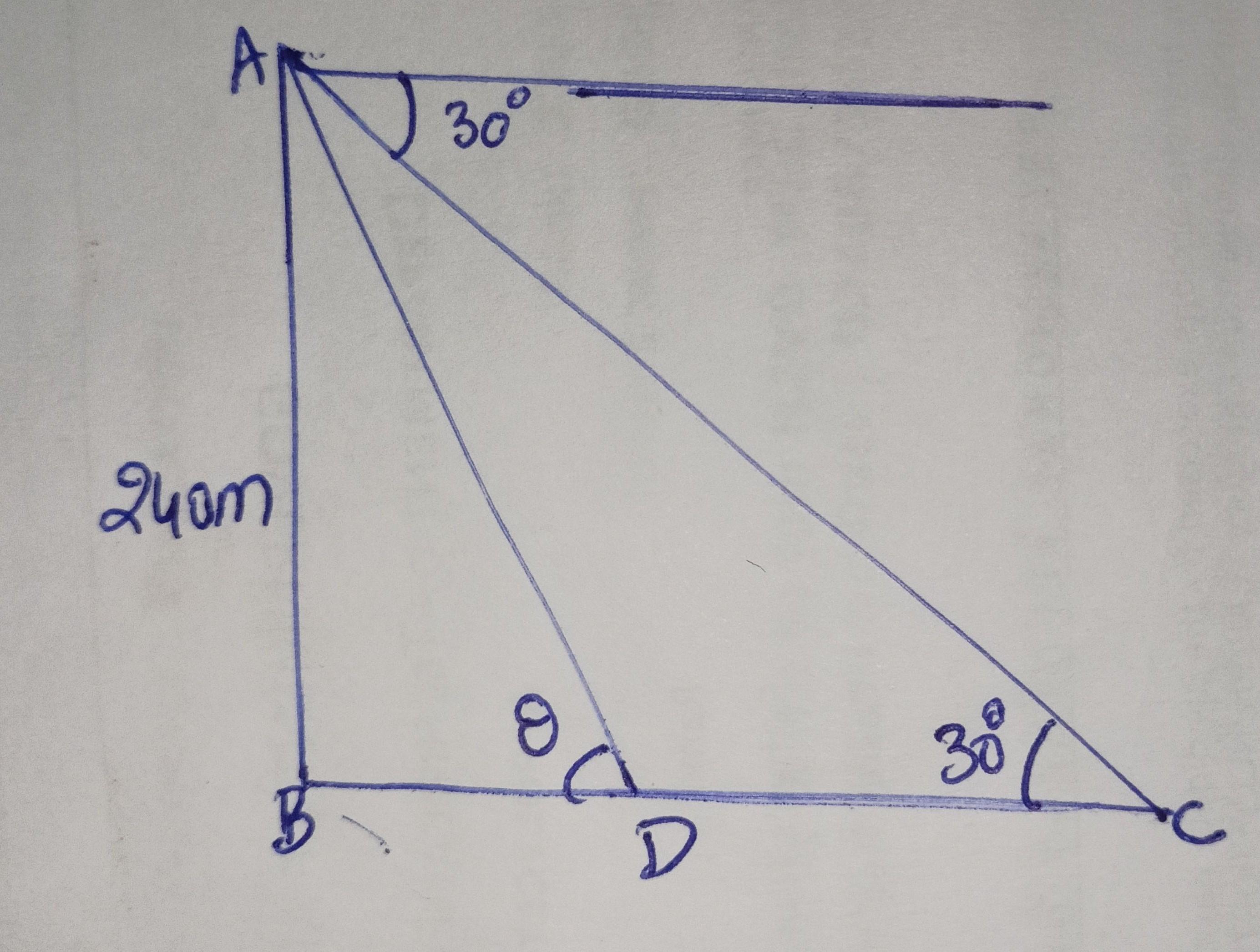
Trigonometry in the form of triangulation forms the basis of navigation , whether is by land, sea or air. gps a radio navigation system helps to locate our position on the earth with the help of satellites. a guard stationed at the top of a 240 m tower observed an unidentified boat coming towards it. a clinometer or inclinometer an instrument used for measuring angles or slopes. the guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30˚ i) make a labelled figure on the basis of given information and calculate the distance the boat from the foot of the observation tower. ii)after 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 -1) m. he immediately raised the alarm what was new angle of depression of the boat from the top of observation tower.
Answers 2
Answer:
i) distance of the boat from the foot of the lighthouse = 240√3m
ii) new angle of depression of the boat = 45°
-
Author:
donutkjhx
-
Rate an answer:
0
Answer:
New angle of depression of the boat from the top of observation tower is 45°
Step-by-step explanation:
height of the tower is
[tex]240m[/tex]
The angle of depression of the boat coming towards the lighthouse and found it to be 30˚
i) The a labelled figure on the basis of given information and the distance the boat from the foot of the observation tower is as follows
in triangle ABC
angel ACB= Tan 30˚
Tan C =
[tex] \frac{ab}{bc} [/tex]
Tan 30˚=
[tex] \frac{240}{bc} [/tex]
=
[tex] \frac{1}{ \sqrt{3} } = \frac{240}{bc} [/tex]
BC=
[tex]240 \sqrt{3} [/tex]
ii)after 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 -1) m.
Actual distance is =
[tex] = 24 \sqrt{3 } - 240 \sqrt{3} + 24 0| [/tex]
[tex] = 240[/tex]
From triangle ABC
Tan D
[tex] = \frac{ab}{bd} [/tex]
Tan D
[tex] = \frac{240}{240} \\ = 1[/tex]
{tan45°=1}
Tan D= Tan 1
D=1
New angle of depression of the boat from the top of observation tower is 45°
-
Author:
keenandulp
-
Rate an answer:
9
If you know the answer add it here!
Other related questions that may help you
-
Author:
sarge
-
Author:
cassandrawaxw
-
Rate an answer:
7
-
Author:
rhett13
-
Author:
kaelynljco
-
Rate an answer:
0
-
Author:
guillermoajep
-
Rate an answer:
18
-
Author:
collin
Answer:
Here is the answer.
Hope it helps.
-
Author:
bebev5jo
-
Rate an answer:
16
-
Author:
sweet 'n sourcerz
-
Rate an answer:
1
-
Author:
adonisfinley
-
Author:
vicentamack
-
Rate an answer:
1