Answers 2
Answer:
The Collatz conjecture states that the orbit of every number under f eventually reaches 1. And while no one has proved the conjecture, it has been verified for every number less than 268. So if you're looking for a counterexample, you can start around 300 quintillion.Step-by-step explanation:
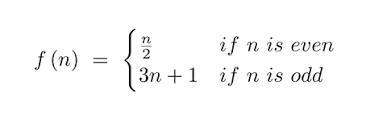
-
Author:
ruchusschmitt
-
Rate an answer:
19
For the first segmentation of this equation "n/2 if n is even." This always leads to 1. There is a fairly simple cause for this. Every even number is necessarily a composite number, with its smallest multiple being 2. For this reason, indefinite division of any even number will always produce 2. Any division of a 2 will absolutely bring 1. For the second segmentation of this equation "f(n) = 3n+1 if n is odd." The distance of an even number from that of an odd number remains constant. This is due to an even number being in all positions that are a composite of 2. I.e. 2nd, 4th, 6th, 8th, 10th, etc. For a value to be odd it must be in a position that is NOT a composite of 2. I.e. 1st, 3rd, 5th, 7th, etc. What this does is puts an unchanging distance of 1 between all odd and all even values. Any odd number multiplied by 3 (of ITS value) will be a composite of that value before multiplication and therefore odd. E.g. 3 multiplied by 3, is 9. And 9 is a composite of 3. But! With the addition of 1 to that odd number, 9 + 1. (as mentioned above) will transfer it to an even position, 10th. Thus initiating the first segmentation of this text and achieving 1. This is general proof of the Collatz Conjecture.
-
Author:
studuufk
-
Rate an answer:
7
