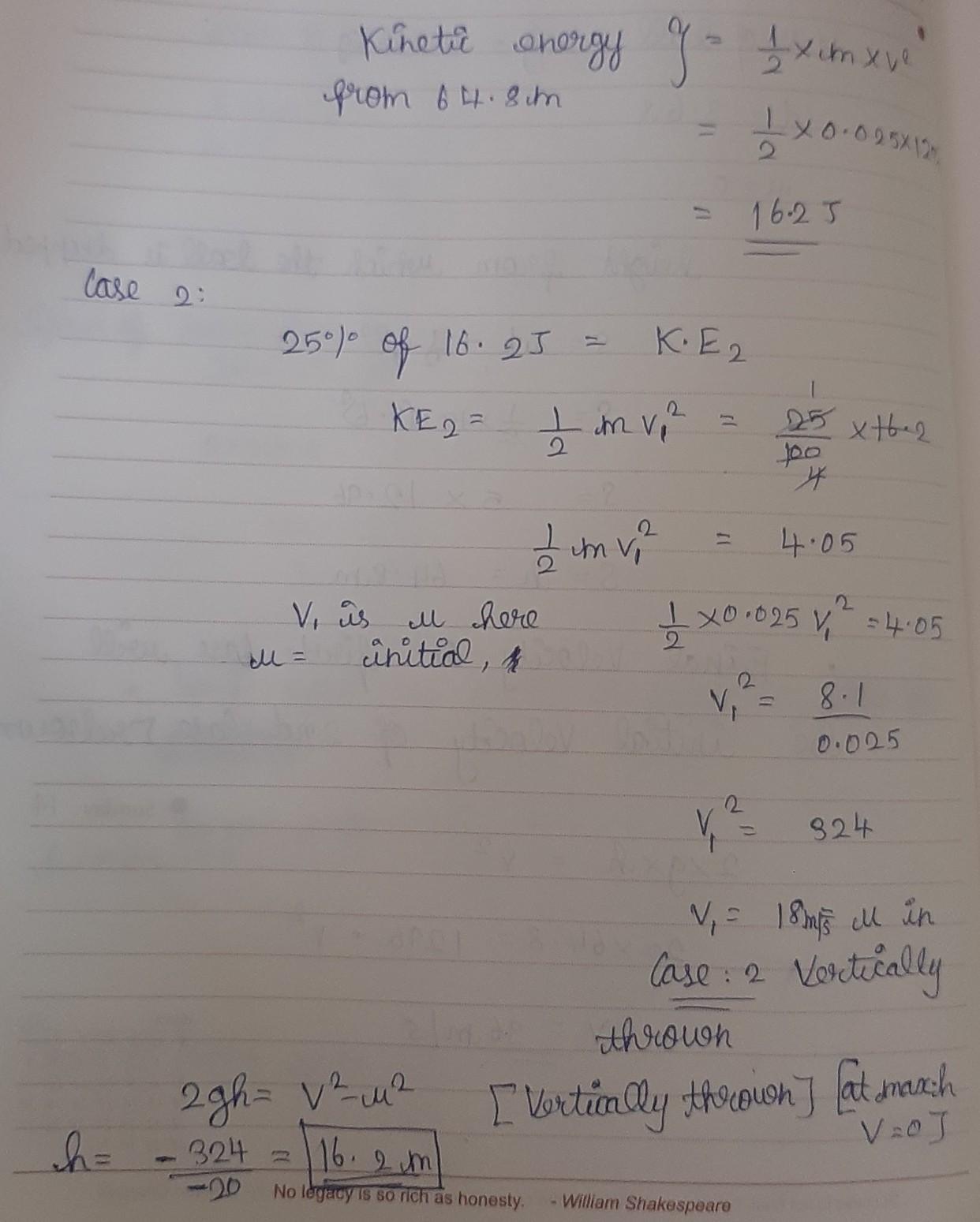गंगा नदीचा उगम कोठे होतो ​

Answer:

You can go to a specific record in Access when you know which record you want to find. The Go to box lets you choose a particular record from a drop-down list and is usually added to forms. To navigate to a specific record, click the arrow to the right of the Go to box, and then select a record from the drop-down list.

Answer:

✨I don't know sorry to say but i don't know✨

Answer:

(1) 0.1n2+7.7n-7.8

(2) 8.2cm

Step-by-step explanation:

plz mark me as brainliest

Answer:

Concept:

Any straight line segment that goes through the centre of the circle and whose endpoints are on the circle is called a diameter of a circle in geometry. It's also known as the longest chord in the circle. For the diameter of a sphere, both definitions are correct. The diameter is also known as the length d of a diameter in modern use. Because all diameters of a circle or sphere have the same length, which is twice the radius r, one speaks of the diameter rather than a diameter in this context.

Given:

(i) Find Sn-1.

(ii) When one tissue sheet is rolled over the roll, what is the diameter?

Find:

we have to find answers for the given questions

Solution:

The solution is

Answer:

16.2 m

Explanation:

pls check the pics

for step by step explanation

also it was a very interesting question for a class 9 student like me

pls mark me brainliest

Answer:

The correct answer is 1.55m.

Explanation:

The time taken by the ball to reach the ground is denoted by t.

the acceleration due to gravity is denoted by a.

The initial speed is denoted by u.

The kinetic energy of the ball just after the ball hit the ground is denoted by [tex]KE_{a}[/tex]  .

The speed of the ball just after the ball hit the ground is denoted by [tex]u_{a}[/tex].

The mass of the ball is denoted by m.

The height attained by the ball when the ball rebounds from the ground is denoted by h.

The final speed of the ball at a height h is denoted by  [tex]v_{a}[/tex].

The velocity of the ball hitting the ground,

[tex]v=u-at[/tex]

[tex]v=0-9.8[/tex]×3.6

v = -35.28m/sec

The kinetic energy of the ball before the ball hit the ground,

[tex]KE_{b} =\frac{1}{2}mv^{2}[/tex]

[tex]KE_{b} =\frac{1}{2}[/tex]×0.025×[tex](-35.28)^{2}[/tex]

[tex]KE_{b}[/tex] = 15.55J

As given in the question,

[tex]KE_{a}=[/tex] 75% of [tex]KE_{b}[/tex]

[tex]\frac{1}{2}mu_{a} ^{2}=\frac{75}{100}[/tex]×15.55

[tex]\frac{1}{2}[/tex]×0.025×[tex]u_{a} ^{2}=\frac{75}{100}[/tex]×15.55

[tex]u_{a}[/tex] = 30.54m/sec

The final speed [tex]v_{a}[/tex] of the ball at a height of h is equal to zero.

By the equation,

[tex]v_{a}=u_{a}-2ah[/tex]

0 = 30.54 - 2 × 9.8 × h

h = 1.55m

So, the height attained by the ball when the ball rebounds from the ground is equal to 1.55m.