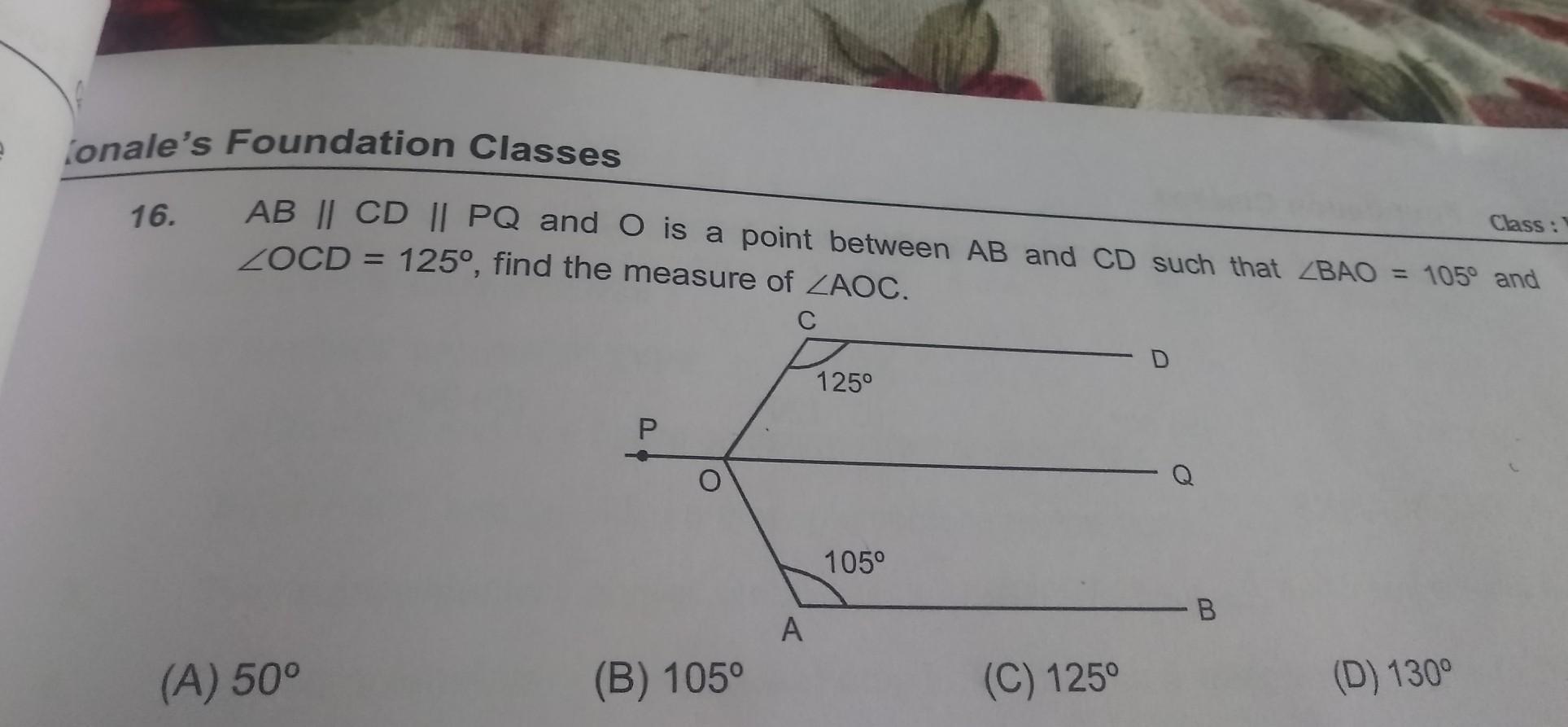
) दिए गए व्याकरण पर आधारित बहुविकल्पीय प्रश्नों के सही उत्तर लीखिए- 1) सही संयुक्त व्यंजन (वर्णमाला के क्रमानुसार ) कौन सा है? क) ज्ञत्र क्ष ख) क्ष त्र ज्ञ ग) त्र क्ष ज्ञ
Answers 1
Answer:
हिंदी वर्णमाला के अनुसार सही क्रम है (ख)क्ष त्र ज्ञ
-
Author:
max3ebo
-
Rate an answer:
9
If you know the answer add it here!
Choose a language and a region
How much to ban the user?
1 hour
1 day
100 years