जास्वमन- तुम्ही केलेल्या गिर्यारोहणाचा गिर्यारोहणाचा अनुभव तुमच्या शब्दोच लिध-​

The atmosphere is held to the earth by the force of gravity. (option b)

Earth is surrounded by a realm of air which is known as the atmosphere. In order to keep this atmosphere attached to the surface of the earth, it exerts an attractive pressure towards the atmosphere and makes the atmosphere appear dense. This force of attraction is known as gravitational force or in simpler terms gravity of the earth.

Energy = 600J

Increase = 100J

To find work done

As we know that Work done can be found with formulas for energy i.e. mv^2/2 and mgh.

Therefore work done = 700J

Answer:

dQ=heat given to system=600

dU=internal ebnergy increased by system=100

dW=work done by system=?

according to fist law of thermodinamics,

dQ=dU-dW

   (or)

dW=dQ-dW

substuting values

dW=600-100 J

     =500 J

Answer:

Solution. Angular S.H.M. is defined as the oscillatory motion of a body in which the torque for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.

Answer:

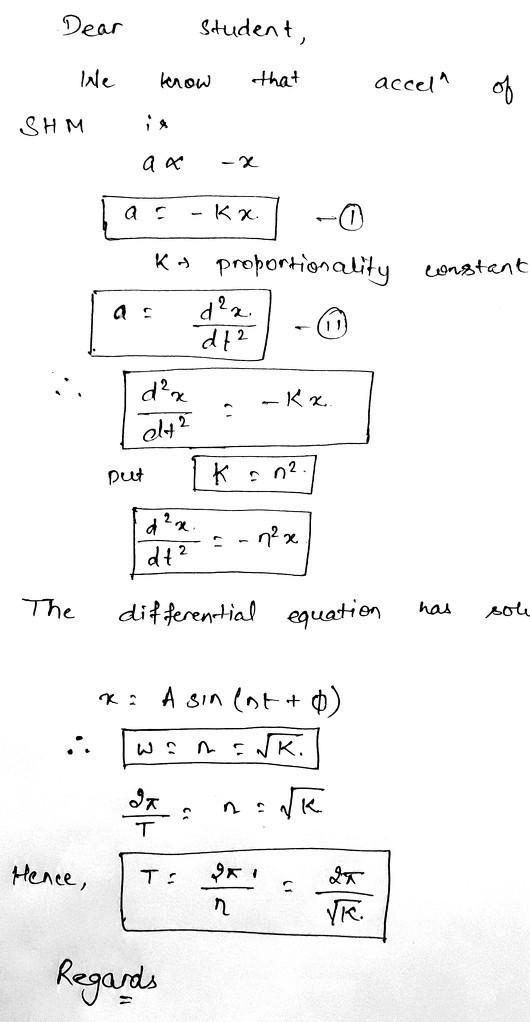
The differential equation of angular SHM is [tex]$\mathrm{I} \frac{d^{2} \theta}{d t^{2}}+c \theta=0[/tex]

Explanation:

• Angular SHM is defined as the oscillatory motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.

The differential equation of angular SHM is

[tex]$\mathrm{I} \frac{d^{2} \theta}{d t^{2}}+c \theta=0 \ldots(1)$$[/tex]

where[tex]$I=$[/tex] moment of inertia of the where [tex]$I=$[/tex] moment of inertia of the oscillating body,

[tex]$\frac{d^{2} \theta}{d t^{2}}=$[/tex]angular acceleration of the body when its angular displacement is [tex]$\theta$[/tex], and [tex]$c=$[/tex] torsion constant of the suspension wire,

[tex]$$\therefore \frac{d^{2} \theta}{d t^{2}}+\frac{c}{I} \theta=0$$[/tex]

Let [tex]$\frac{c}{I}=\omega^{2}$[/tex], a constant. Therefore the angular frequency, [tex]$\omega=\sqrt{\frac{c}{I}}$[/tex] and the angular acceleration,

[tex]$\mathrm{a}=\frac{d^{2} \theta}{d t^{2}}=-\omega^{2} \theta \ldots(2)$$[/tex]

The minus sign shows that the [tex]$\propto$[/tex] and [tex]$\theta$[/tex] have opposite directions. The period [tex]$T$[/tex]of angular SHM is

[tex]$\mathrm{T}=\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{C}{I}}}=2 \pi \sqrt{\frac{I}{C}} \ldots . .(3)$$[/tex]

This is the expression for the period terms of torque constant. Also from Eq.(2),

[tex]$$\omega=\sqrt{\left|\frac{x}{\theta}\right|}$$[/tex]

[tex]$=\sqrt{\text { angular acceleration per unit angular displacement }}$[/tex]

[tex]\begin{aligned}&\therefore \top=\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\left|\frac{\alpha}{\theta}\right|}} \\&=\frac{2 \pi}{\sqrt{\text { angularacceleration per unit angulardisplacement }}}\end{aligned}[/tex]

Conditions for an Angular Oscillation to be Angular SHM

The body must experience a net Torque that is restoring in nature. If the angle of oscillation is small, this restoring torque will be directly proportional to the angular displacement.

[tex]$T \propto-\theta$[/tex]

[tex]$$\mathrm{T}=-\mathrm{k} \theta$$[/tex]

[tex]$$T=1 \alpha$$[/tex]

[tex]$$\begin{aligned}&\alpha=-\mathrm{k} \theta \\&I \frac{d^{2} \theta}{d t^{2}}=-K \theta\end{aligned}$$[/tex]

[tex]$\frac{d^{2} \theta}{d t^{2}}=-\left(\frac{K}{I}\right) \theta=-\omega_{0}^{2} \theta$$[/tex]

[tex]$\frac{d^{2} \theta}{d t^{2}}=-\omega_{0}^{2} \theta=0$$[/tex]

This is the differential equation of an angular Simple Harmonic Motion. Solution of this equation is angular position of the particle with respect to time.

[tex]$$\theta=\theta_{0} \sin \left(\omega_{0} t+\phi\right)$$[/tex]

Then angular velocity,

[tex]$$\omega=\theta_{0} \cdot \omega_{0} \cos \left(\omega_{0} t+\phi\right)$$[/tex]

[tex]$\theta_{0}$[/tex]- amplitude of the angular SHM

Learn about angular simple harmonic motion

• https://brainly.in/question/7642032?referrer=searchResults
• https://brainly.in/question/7642005?referrer=searchResults

Answer:

ekTara , khol , mandira , banshi were musical instruments

The ektara,khol,banshi,mandira were

a.popular folk musical instruments from bengal

b. Popular ragas from bengal

c. poular folk dance forms from bengal

Explanation:

Popular folk musical instruments from Bengal.