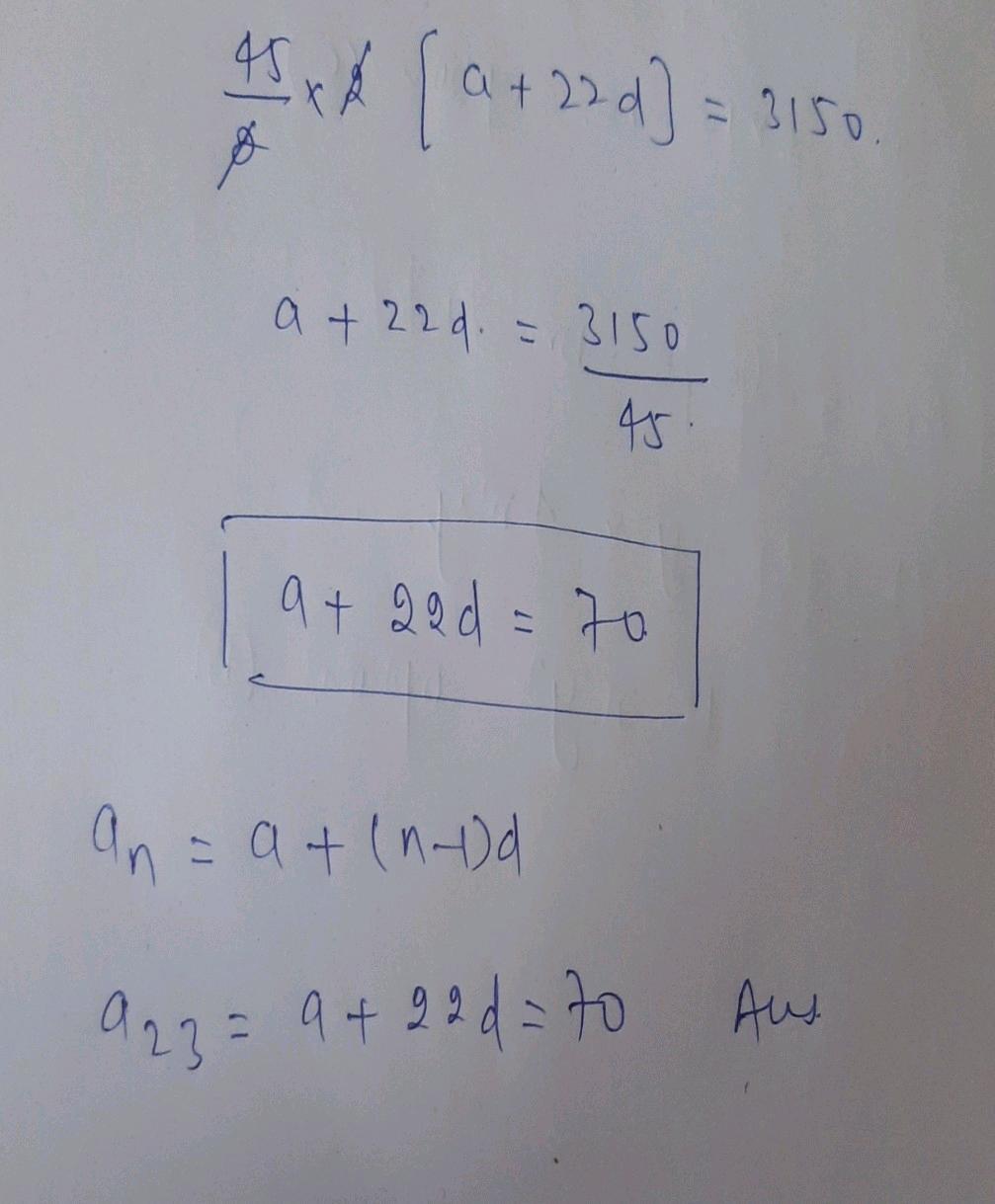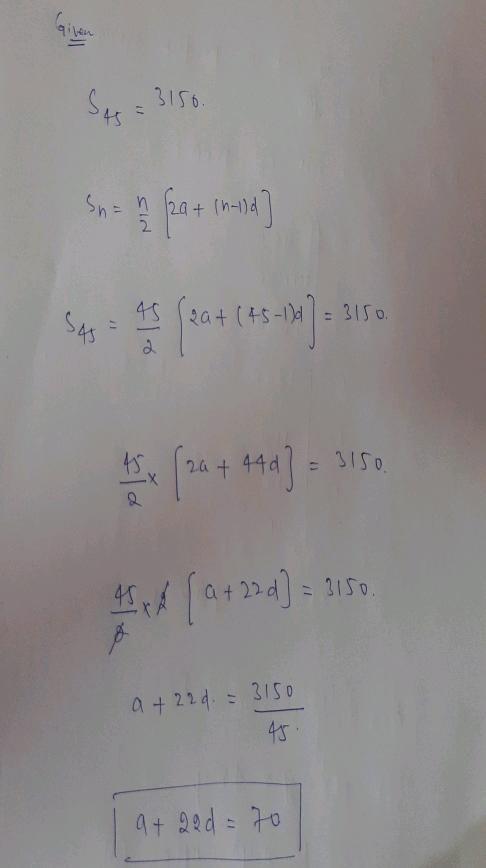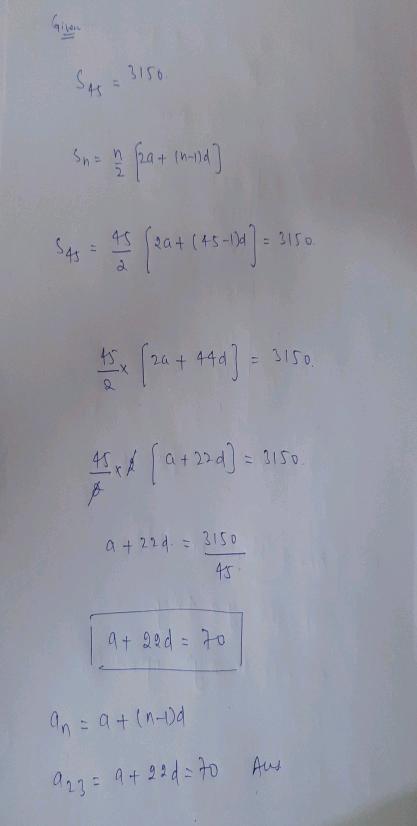What is the meaning of Adorable baby??​

Answer:

6. meera had maded a record

Answer:

passive or active ??????????

Answer:

d = 1

Step-by-step explanation:

A17 = a + 16d

A10 = a + 9d

A17 = a + 9d + 7

a + 16 d = a + 9d + 7 ( a gets cancelled out both sides)

16 d - 9 d = 7

7 d = 7

d = 1

Please mark it as Brainliest answer !

Step-by-step explanation:

Answer:

[tex]\boxed{ \sf{ \:\bf Length\:of\:Latus\:Rectum = \dfrac{ |2(la + mb + n) |}{ \sqrt{ {l}^{2}+{m}^{2} } } \: }} \\ \\ [/tex]

Step-by-step explanation:

Given that,

Focus of parabola is (a, b)

Equation of directrix : lx + my + n = 0

We have to find the length of the lactus rectum of the parabola, if the equation of the directrix lx + my + n = 0 and the focus of the parabola (a, b).

We know,

Length of latus rectum = 2 × ( Length of perpendicular drawn from focus on the directrix)

i.e.

Length of latus rectum = 2 × ( Length of perpendicular drawn from (a, b) on the line lx + my + n = 0)

So,

[tex]\sf \: Length\:of\:Latus\:Rectum = 2\bigg |\dfrac{la + mb + n}{ \sqrt{ {l}^{2} + {m}^{2} } } \bigg| \\ \\ [/tex]

Hence,

[tex]\bf\implies Length\:of\:Latus\:Rectum = \dfrac{ |2(la + mb + n) |}{ \sqrt{ {l}^{2}+{m}^{2} } } \\ \\ [/tex]

[tex]\rule{190pt}{2pt}[/tex]

Additional Information

[tex]\begin{gathered}\boxed{\begin{array}{c|c} \bf {y}^{2} = 4ax & \bf \\ \frac{\qquad \qquad}{} & \frac{\qquad \qquad}{} \\ \sf Vertex & \sf (0,0) \\ \\ \sf Focus & \sf (a,0) \\ \\ \sf Length \: of \: latus \: rectum & \sf 4a\\ \\ \sf Equation \: of \: axis & \sf y = 0\\ \\ \sf Equation \: of \: directrix & \sf y = - a \end{array}} \\ \end{gathered} \\ [/tex]

[tex]\begin{gathered}\boxed{\begin{array}{c|c} \bf {y}^{2} = - 4ax & \bf \\ \frac{\qquad \qquad}{} & \frac{\qquad \qquad}{} \\ \sf Vertex & \sf (0,0) \\ \\ \sf Focus & \sf ( - a,0) \\ \\ \sf Length \: of \: latus \: rectum & \sf 4a\\ \\ \sf Equation \: of \: axis & \sf y = 0\\ \\ \sf Equation \: of \: directrix & \sf y = a \end{array}} \\ \end{gathered} \\ [/tex]

[tex]\begin{gathered}\boxed{\begin{array}{c|c} \bf {x}^{2} = 4ay & \bf \\ \frac{\qquad \qquad}{} & \frac{\qquad \qquad}{} \\ \sf Vertex & \sf (0,0) \\ \\ \sf Focus & \sf (0,a) \\ \\ \sf Length \: of \: latus \: rectum & \sf 4a\\ \\ \sf Equation \: of \: axis & \sf x = 0\\ \\ \sf Equation \: of \: directrix & \sf x = - a \end{array}} \\ \end{gathered} \\ [/tex]

[tex]\begin{gathered}\boxed{\begin{array}{c|c} \bf {x}^{2} = \: - \: 4ay & \bf \\ \frac{\qquad \qquad}{} & \frac{\qquad \qquad}{} \\ \sf Vertex & \sf (0,0) \\ \\ \sf Focus & \sf (0, - a) \\ \\ \sf Length \: of \: latus \: rectum & \sf 4a\\ \\ \sf Equation \: of \: axis & \sf x = 0\\ \\ \sf Equation \: of \: directrix & \sf x = a \end{array}} \\ \end{gathered} \\ [/tex]

Answer:

Step-by-step explanation:

attachment there