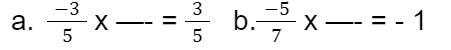• Have you seen any of these stories in TV serials or movies ?​

Answer:

तट

Hope it Helps, Please mark me as the Brainliest

d) Pitra

this is the answer of the question

Answer:

Pitra

Explanation:

this is the answer

Answer:

How cells extract energy from glucose without oxygen. In yeast, the anaerobic reactions make alcohol, while in your muscles, they make lactic acid.

Answer:

The correct answer is C

Lactic acid

Answer:

a -  (-1)

b - (-7/5)

Step-by-step explanation:

Answer:

[tex]\qquad \:\boxed{\begin{aligned}& \qquad \:\sf \:(a) \: - \dfrac{3}{5} \times ( - 1) = \dfrac{3}{5} \qquad \: \\ \\& \qquad \:\sf \: (b) \: - \dfrac{5}{7} \times \dfrac{7}{5} = - 1\end{aligned}} \qquad \\ \\ [/tex]

Step-by-step explanation:

[tex]\large\underline{\sf{Solution-a}}[/tex]

Given expression is

[tex]\sf \: - \dfrac{3}{5} \times ...... = \dfrac{3}{5} \\ \\ [/tex]

Let assume that missing number be x.

So,

[tex]\sf \: - \dfrac{3}{5} \times x = \dfrac{3}{5} \\ \\ [/tex]

[tex]\sf \: x = \dfrac{3}{5} \div \bigg( - \dfrac{3}{5} \bigg) \\ \\ [/tex]

[tex]\sf \: x = - \: \dfrac{3}{5} \div \bigg( \dfrac{3}{5} \bigg) \\ \\ [/tex]

[tex]\sf \: x = - \: \dfrac{3}{5} \times \dfrac{5}{3} \\ \\ [/tex]

[tex]\sf\implies \sf \: x = - \: 1 \\ \\ [/tex]

Hence,

[tex]\sf\implies \bf \: - \dfrac{3}{5} \times ( - 1) = \dfrac{3}{5} \\ \\ [/tex]

[tex]\large\underline{\sf{Solution-b}}[/tex]

[tex]\sf \: - \dfrac{5}{7} \times ...... = - 1 \\ \\ [/tex]

Let missing number be x

[tex]\sf \: - \dfrac{5}{7} \times x = - 1 \\ \\ [/tex]

[tex]\sf \: x = - 1 \div \bigg( - \dfrac{5}{7} \bigg) \\ \\ [/tex]

[tex]\sf \: x = 1 \div \bigg(\dfrac{5}{7} \bigg) \\ \\ [/tex]

[tex]\sf \: x = 1 \times \dfrac{7}{5} \\ \\ [/tex]

[tex]\sf\implies \sf \: x = \dfrac{7}{5} \\ \\ [/tex]

Hence,

[tex]\sf\implies \bf \: - \dfrac{5}{7} \times \dfrac{7}{5} = - 1 \\ \\ [/tex]