what we call window in marathi???​

Answer:

c mouse light pen keyboard

mark me as brainlist if this will help you

Answer:

answer is option c

Explanation:

Mark me as brainilist

Answer:

Solution

verified

Verified by Toppr

Correct option is B)

In this case, the 2 resistors of 3 ohms and 2 ohms on the upper half of the circuit are connected in series and the combined resistance R1 is given as 3+2 = 5 ohms.

The 2 resistors of 6 ohms and 4 ohms on the lower half of the circuit are connected in series and the combined resistance R2 is given as 6+4 = 10 ohms.

The resistances R1, R2 and 30 ohms in the middle are connected in parallel. So the total resistance R of this parallel connection is given as

5

1

+

10

1

+

30

1

=

0.33

1

=3ohms. That is, the resistance in the closed loop is reduced to 3 ohms.

Hence, the value of the resistance in the circuit between A and B is 3 ohms.

Was this answer helpful?

upvote

48

downvote

Explanation:

Answer:

The value of R₁/R₂ is 5/9.

Explanation:

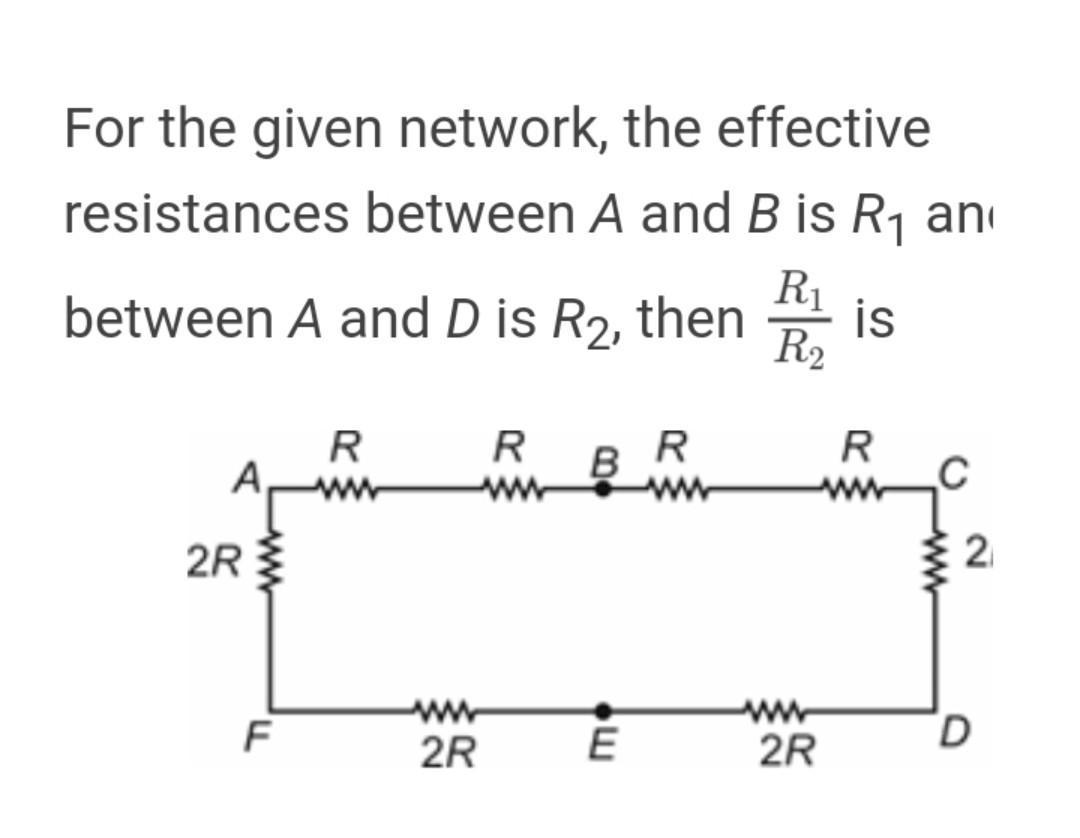
CASE I: Effective resistance between A and B

In this situation, there are two cells of resistance "R" connected in series, and this combination is connected in parallel with the series combination other six cells of resistance "R" and "2R". So,

[tex]R_a=R+R=2R[/tex]

[tex]R_b=2R+2R+2R+2R+R+R=10R[/tex]

Ra and Rb are parallelly connected and their effective resistance is R₁.

[tex]\frac{1}{R_1}=\frac{1}{R_a}+\frac{1}{R_b}[/tex]          (1)

By substituting the value of Ra and Rb in equation (1) we get;

[tex]\frac{1}{R_1}=\frac{1}{2R}+\frac{1}{10R}=\frac{5+1}{10R}=\frac{6}{10R}=\frac{3}{5R}[/tex]

[tex]R_1=\frac{5R}{3}[/tex]                       (2)

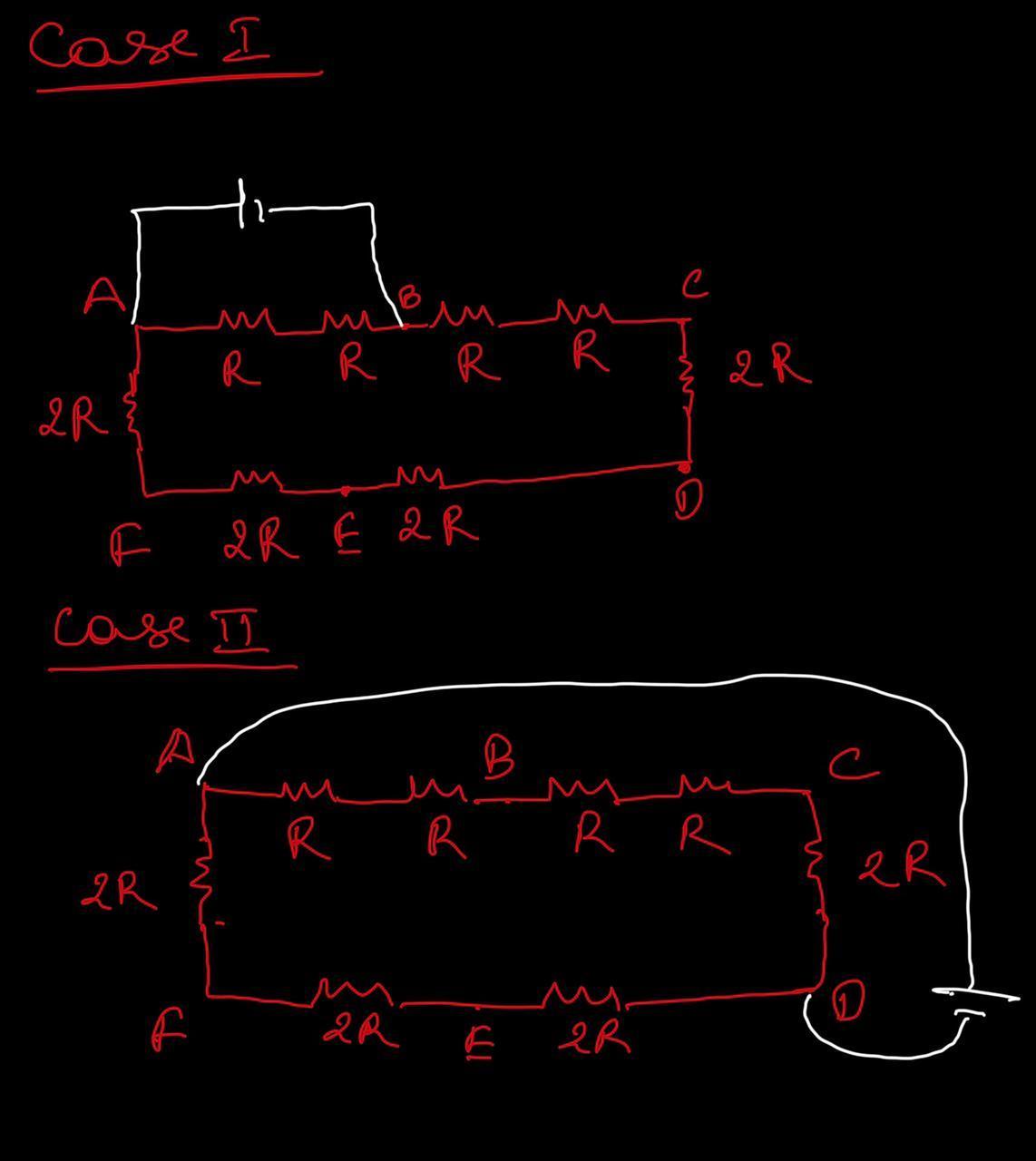
CASE II: Effective resistance between A and D

In this situation, there are five cells of resistance "R" and "2R" connected in series, and this combination is connected in parallel with the series combination of the other three cells of resistance "2R". So,

[tex]R_c=R+R+R+R+2R=6R[/tex]

[tex]R_d=2R+2R+2R=6R[/tex]

Rc and Rb are parallelly connected and their effective resistance is R₂.

[tex]\frac{1}{R_2}=\frac{1}{R_c}+\frac{1}{R_d}[/tex]             (3)

By substituting the value of Rc and Rd in equation (3) we get;

[tex]\frac{1}{R_2}=\frac{1}{6R}+\frac{1}{6R}=\frac{2}{6R}=\frac{1}{3R}[/tex]

[tex]R_2=3R[/tex]                   (4)

As per the question,

[tex]\frac{R_1}{R_2}=\frac{\frac{5R}{3}}{3R}=\frac{5}{9}[/tex]                   (5)

Hence, the value of R₁/R₂ is 5/9.

Answer:

2345 hhaj and to has a mot

16 is the total no of Relations .

Step-1(Formula Used)-

The formula for calculating No of relations =[tex]2^{n^{2} }[/tex] where n is no of elements in the Set..

Step-2(Calculation of relations)

=[tex]2^{2^{2} } =2^{4}=16[/tex]..

Therefore 16 is no of relations..

Answer:

This is your answer

Explanation:

The SA node has the inherent power of generating a wave of contraction and controlling the heartbeat. Thus, it is known as the pacemaker. As the SA node initiates a wave of contraction and controls the heartbeat, the contraction's impulse originates in the heart itself; the human heart is termed myogenic.