Derive an expression for linear velocity at lowest point and at highest point for particle revolving in vertical circular motion

Answers 1

[tex]\huge{\underline{\underline{\mathfrak{Answer :}}}}[/tex]

Let,

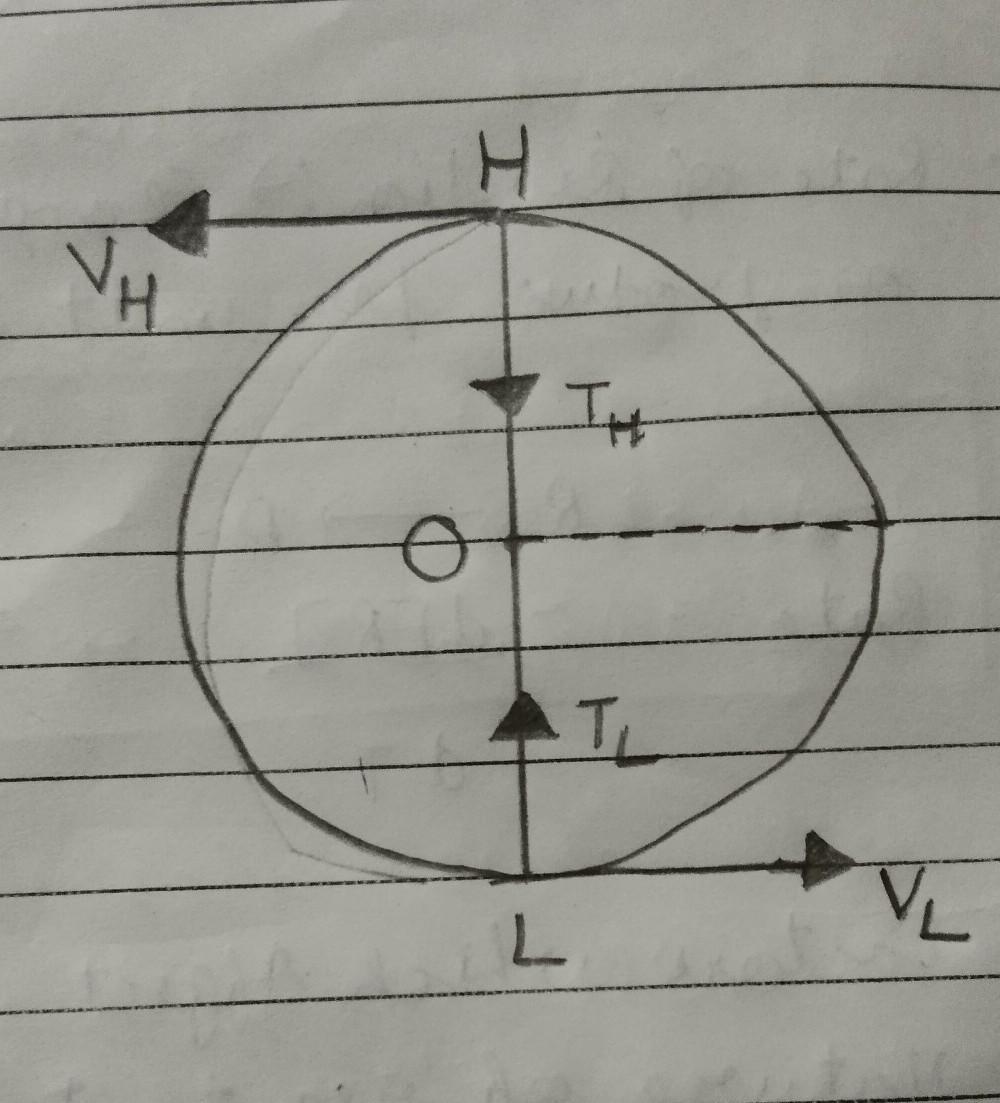
  • [tex]\sf{T_{L}}[/tex] = Tension at the lowest point.
  • [tex]\sf{T_{H}}[/tex] = Tension at the highest point.
  • [tex]\sf{V_{L}}[/tex] = Velocity at the lowest point.
  • [tex]\sf{V_{H}}[/tex] = Velocity at the highest point.

________________________

At lowest point L,

[tex]\sf{\rightarrow T_L = \dfrac{m {v_L}^2}{r} + mg}[/tex] _______(1)

At highest point H,

[tex]\sf{\rightarrow T_L = \dfrac{m {v_H}^2}{r} - mg}[/tex] _______(2)

________________________

Subtracting (1) by (2).

[tex]\sf{\rightarrow T_L - T_H = \dfrac{{mv_L}^2}{r} + mg - (\dfrac{{mv_H}^2}{r} - mg)}[/tex]

[tex]\sf{\rightarrow T_L - T_H = \dfrac{m}{r} ({v_L}^2 - {v_H}^2 + 2mg})[/tex] ______(3)

________________________

By law of conservation of energy,

(P.E + K.E) at L = (P.E + K.E) at H

[tex]\sf{ \therefore 0 + \dfrac{1}{2} {mv_L}^2 = mg.2r + \dfrac{1}{2} {mv_H}^2}[/tex]

[tex]\sf{ \therefore \dfrac{1}{2}m ({v_L}^2 - {v_H}^2) = mg.2r}[/tex]

[tex]\sf{ \therefore {v_L}^2 - {v_H}^2 = 4gr}[/tex]_______(4)

________________________

From equation (3) and (4),

[tex]\sf{\rightarrow T_L - T_H = \dfrac{m}{r}(4gr) + 2mg}[/tex]

[tex]\sf{\rightarrow T_L - T_H = 4mg + 2mg}[/tex]

[tex]\bf{ \therefore T_L - T_H = 6mg}[/tex]

answer img

If you know the answer add it here!

Can't find the answer?

Other related questions that may help you

A ship leaves a harbor and sails 125km on a bearing of 080°. the ship then sails 85km on a bearing of 145°. a make a scale drawing of the ship’s journey. [03] b how far must the ship now sail in a straight line to return to the harbor? [01] c on what bearing must the ship now sail to return to the harbor? [02] tip use a scale of 1cm to represent 10km

Answer:

160 km per hour in that day

what is the national dance of Saudi Arabia?​

Answer:

the ardha

Dance is also popular among Saudis. The national dance is the men's sword dance known as the ardha. An ancient tradition with its roots in the country's central area known as the Najd, the ardha is a combination of singers, dancers carrying swords and a poet or narrator.
Who owns the IP rights in a work product created by an employee during his/her tenur Infosys? Oa. a. Employee b. Employer Oc. Both employee & employer Od. Government​

Answer:

With this investment, it should come as no surprise that employers generally own the intellectual property created by its employees in the course of their employment. However, intellectual property that is created by an employee, other than in the course of employment, is owned by the employee not the employer.

Akshat is a class 10 student. He went to his grandparent's home in a village. His grandfather took him to the bank of a nearby river. Akshat was very happy to see the pollution-free village environment. He was standing on the bank of the river observed that the angle of elevation of the top of a tree standing on the opposite bank was 60°. When he moved 30 metres away from the bank, he found the angle of elevation to be 30° .Find the height of the tree.Find the width of the river. [Take √3= 1.732.]​

Answer:

THE ANSWER IS

HEIGHT OF THE TREE= 26m

WIDTH OF THE RIVER= 15m

Step-by-step explanation:

let the width of the river be x and the height of the tree be h.

h/30+x= 1/root3--------(1)

h/x=root3-------(2)

after solving both equations we get,

30+x=3x

30=2x

x=15  (width of the river)

after substituting the value of x in equation 2 we get h= 25.96m which is equal to 26m.

Answer:

height of the tree is 15m

width of the river is 25.98

answer img

Other Accountancy Questions

Log in with Google

 or

Forgot your password?

I don't have an account, and I want to Register

Choose a language and a region

English

United States

Polski

Polska

Português

Brasil

English

India

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Türkçe

Türkiye
How much to ban the user?
1 hour 1 day 100 years